 , πολυώνυμο άρτιου βαθμού, για το οποίο ισχύει
, πολυώνυμο άρτιου βαθμού, για το οποίο ισχύει  .
.Να αποδείξετε ότι
 για κάθε
για κάθε 
Συντονιστές: achilleas, emouroukos, silouan
 , πολυώνυμο άρτιου βαθμού, για το οποίο ισχύει
, πολυώνυμο άρτιου βαθμού, για το οποίο ισχύει  .
. για κάθε
για κάθε 
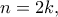 όπου
όπου  με
με  . Δίχως βλάβη της γενικότητας, υποθέτουμε ότι
. Δίχως βλάβη της γενικότητας, υποθέτουμε ότι 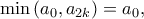 οπότε η δοσμένη σχέση γράφεται ισοδύναμα:
οπότε η δοσμένη σχέση γράφεται ισοδύναμα: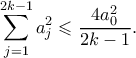

 . Έχουμε ότι:
. Έχουμε ότι:


 έχουμε ότι:
έχουμε ότι:


 , ότι:
, ότι:
 ισχύει:
ισχύει: 
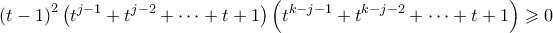 )
)





 είναι διαφορετικά τότε
είναι διαφορετικά τότε 
 τότε το πολυώνυμο μπορεί να έχει ρίζα το
τότε το πολυώνυμο μπορεί να έχει ρίζα το  η το
η το  .
.
 , θεωρούμε το πολυώνυμο
, θεωρούμε το πολυώνυμο 


![\displaystyle{Q(y)=(y-1)^2\left[(2N-1)y^{2N-2}+(4N-6)y^{2N-3}+\cdots +(2N-1)\right]\geq 0.} \displaystyle{Q(y)=(y-1)^2\left[(2N-1)y^{2N-2}+(4N-6)y^{2N-3}+\cdots +(2N-1)\right]\geq 0.}](/forum/ext/geomar/texintegr/latexrender/pictures/76bc69bc925fcd59b5be3a6c984f1d9e.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες