 μη αρνητικοί να αποδείξετε
μη αρνητικοί να αποδείξετε![(2x+y)(2z+x)(2y+z)(2x+z)(2y+x)(2z+y)\geq 8[(x+y)(y+z)(z+y)]^{2} (2x+y)(2z+x)(2y+z)(2x+z)(2y+x)(2z+y)\geq 8[(x+y)(y+z)(z+y)]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/53b6a5ad19943f7efd51632df735dd8c.png)
Συντονιστές: achilleas, emouroukos, silouan
Για
 μη αρνητικούς, έχουμε:
μη αρνητικούς, έχουμε: 
 ,
,  και
και  .
.![(2x+y)(2z+x)(2y+z)(2x+z)(2y+x)(2z+y)\geq 8[(x+y)(y+z)(z+x)]^{2} (2x+y)(2z+x)(2y+z)(2x+z)(2y+x)(2z+y)\geq 8[(x+y)(y+z)(z+x)]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/f3dc6de1be5d1e5a0e4e36f214eef433.png)
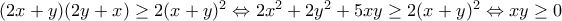 που ισχύει με ισότητα όταν αν ένας από τους
που ισχύει με ισότητα όταν αν ένας από τους 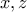 είναι
είναι  .
. και
και  άρα πολλαπλασιάζοντας κατά μέλη παίρνουμε την ζητούμενη ανισότητα.
άρα πολλαπλασιάζοντας κατά μέλη παίρνουμε την ζητούμενη ανισότητα. που για να ικανοποιείται αρκεί
που για να ικανοποιείται αρκεί  από τους
από τους  να είναι ίσοι με
να είναι ίσοι με  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες