 είναι θετικοί πραγματικοί και
είναι θετικοί πραγματικοί και 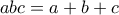 να αποδειχθεί ότι:
να αποδειχθεί ότι: 
Συντονιστές: achilleas, emouroukos, silouan
 είναι θετικοί πραγματικοί και
είναι θετικοί πραγματικοί και 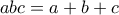 να αποδειχθεί ότι:
να αποδειχθεί ότι: 
ΑνΔιονύσιος Αδαμόπουλος έγραψε:Ανείναι θετικοί πραγματικοί και
να αποδειχθεί ότι:
 τότε
τότε  χάσαμε και ομια για τα άλλα.
χάσαμε και ομια για τα άλλα.  με
με  οξείες γωνίες
οξείες γωνίες 
 είναι γωνίες τριγώνου.
είναι γωνίες τριγώνου.
Εύκολη απόδειξη πχ με Jensen...ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:ΑνΔιονύσιος Αδαμόπουλος έγραψε:Ανείναι θετικοί πραγματικοί και
να αποδειχθεί ότι:
τότε
χάσαμε και ομια για τα άλλα.
Ετσι θέτονταςμε
οξείες γωνίες
έχουμε
δηλαδή ταείναι γωνίες τριγώνου.
Η προς απόδειξη γράφεται
που είναι γνωστή .
(το 1977 την είχαν σχεδόν όλα τα βιβλία τριγωνομετρίας
 .
.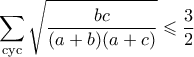 .
.
 .
. .
.Ορέστη, αν και δεν είμαι ο θεματοδότης ... Πολύ ωραία λύση!!Ορέστης Λιγνός έγραψε:Γεια σου Διονύση.
Είναι
.
Αρκεί λοιπόν.
Όμως, από AM-GM,
.
Η ισότητα αν.
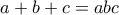 σε
σε  όπου κερδίζουμε:
όπου κερδίζουμε:  σε συνάρτηση με τα
σε συνάρτηση με τα 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες