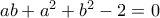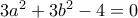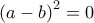nsmavrogiannis έγραψε:Δίνεται η συνάρτηση
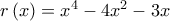
. Να βρεθεί ευθεία που να είναι εφαπτομένη της γραφικής παράστασης της

σε δύο διαφορετικά σημεία.
1ος τρόπος:
Είναι

. Η ευθεία που εφάπτεται στη γραφική παράσταση της

σε δυο διαφορετικά σημεία είναι προφανώς ο

-άξονας. Συνεπώς, η ζητούμενη ευθεία είναι η
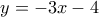
.
2ος τρόπος:
Η ευθεία

τέμνει τη γραφική παράσταση της συνάρτησης

το πολύ σε δυο σημεία αν και μόνο αν η γραφική παράσταση του πολυωνύμου
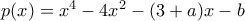
τέμνει τον

-άξονα σε δυο σημεία, δηλαδή, το πολυώνυμο έχει δυο πολλαπλές ρίζες. Εφόσον είναι βαθμού τέσσερα, η πολλαπλότητα κάθε ρίζας είναι δυο, κι άρα δεν υπάρχουν άλλες ρίζες. Αν οι ρίζες είναι

,

, τότε είναι

.
Κάνοντας τις πράξεις στο δεύτερο μέλος

κι εξισώνοντας τους αντίστοιχους συντελεστές παίρνουμε
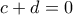 (1)
(1)
 (2)
(2)
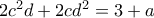 (3)
(3)
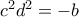
(4)
Από (1), (3) έπεται ότι

κι από (1), (2), ότι
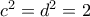
, που σε συνδυασμό με την (4) δίνει
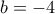
.
Συνεπώς, η (μόνη) ζητούμενη ευθεία είναι η
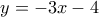
.
Παρατήρηση: Τουλάχιστον ακόμη ένας τρόπος μπορεί να δοθεί χρησιμοποιώντας παραγώγους. Δείτε και το παρόμοιο πρόβλημα Β3470 του KoMal
http://www.komal.hu/lap/2002-ang/b3470.e.shtml
Φιλικά,
Αχιλλέας
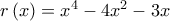 . Να βρεθεί ευθεία που να είναι εφαπτομένη της γραφικής παράστασης της
. Να βρεθεί ευθεία που να είναι εφαπτομένη της γραφικής παράστασης της  σε δύο διαφορετικά σημεία.
σε δύο διαφορετικά σημεία.
 . Η ευθεία που εφάπτεται στη γραφική παράσταση της
. Η ευθεία που εφάπτεται στη γραφική παράσταση της  σε δυο διαφορετικά σημεία είναι προφανώς ο
σε δυο διαφορετικά σημεία είναι προφανώς ο  -άξονας. Συνεπώς, η ζητούμενη ευθεία είναι η
-άξονας. Συνεπώς, η ζητούμενη ευθεία είναι η 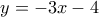 .
. τέμνει τη γραφική παράσταση της συνάρτησης
τέμνει τη γραφική παράσταση της συνάρτησης  το πολύ σε δυο σημεία αν και μόνο αν η γραφική παράσταση του πολυωνύμου
το πολύ σε δυο σημεία αν και μόνο αν η γραφική παράσταση του πολυωνύμου 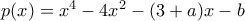 τέμνει τον
τέμνει τον  ,
,  , τότε είναι
, τότε είναι  .
.
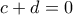

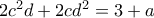
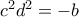 (4)
(4) κι από (1), (2), ότι
κι από (1), (2), ότι 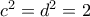 , που σε συνδυασμό με την (4) δίνει
, που σε συνδυασμό με την (4) δίνει 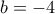 .
.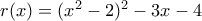 " και να συνεχίσουμε αποδεικνύοντας ότι η
" και να συνεχίσουμε αποδεικνύοντας ότι η 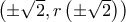
 με
με  παραγωγίσιμες και
παραγωγίσιμες και  είναι μια οποιαδήποτε ρίζα της
είναι μια οποιαδήποτε ρίζα της  τότε η
τότε η  στο σημείο
στο σημείο 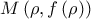
 και έχει την σωστή κλίση αφού με παραγώγιση βρίσκουμε
και έχει την σωστή κλίση αφού με παραγώγιση βρίσκουμε 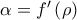 .
. b και για την κοινή εφαπτομένη ε ισχύει (τύπος σχολικού βιβλίου κατεύθυνσης):
b και για την κοινή εφαπτομένη ε ισχύει (τύπος σχολικού βιβλίου κατεύθυνσης): r'(b)x+r(b)-br'(b).
r'(b)x+r(b)-br'(b).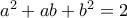 και από την δεύτερη
και από την δεύτερη  (ελπίζω να απέφυγα αριθμητικά λάθη).
(ελπίζω να απέφυγα αριθμητικά λάθη). .
. 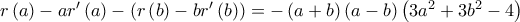
 χρειάζεται να αποκλείσουμε την περίπτωση
χρειάζεται να αποκλείσουμε την περίπτωση