Tolaso J Kos έγραψε:Δίδονται οι συναρτήσεις

με

όπου

α)Να δειχθεί ότι

β)Αν η ελάχιστη τιμή της διαμέσου των παρατηρήσεων

είναι

τότε:
i)να βρεθεί η τιμή του

ii)Έστω ο δειγματικός

όπου οι πιθανότητες
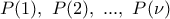
των στοιχειωδών ενδεχομένων είναι διαδοχικοί όροι γεωμετρικής προόδου με λόγο

. Θεωρούμε τα ενδεχόμενα:

: το

τέτοιο ώστε η εφαπτομένη της

στο

να διέρχεται από την αρχή των αξόνων.

: το

τέτοιο ώστε η

να έχει δύο άνισες πραγματικές ρίζες.
Να οριστεί η

ΛΥΣΗ
α) Είναι

και

άρα

β)
i)Προφανώς λόγω (α)

άρα οι παρατηρήσεις κατά αύξουσα σειρά είναι

και αν

τότε

και για την συνάρτηση

που είναι παραγωγίσιμη με


και επειδή είναι

και
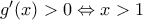
και

η

έχει ελάχιστη τιμή για

την
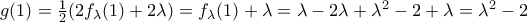
θέλουμε να είναι

και αν

τότε

και για την

που είναι παραγωγίσιμη με
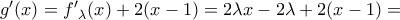
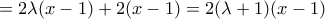
και όπως προηγούμενα έχει ελάχιστη τιμή

θέλουμε να είναι

που είναι αδύνατη γιατί θέλουμε να είναι

Άρα δεκτή η

οπότε

ii) Είναι τώρα

και ισχύει ότι

και αφού είναι άθροισμα διαδοχικών όρων γεωμετρικής προόδου με λόγο

θα ισχύει ότι

επομένως

Τώρα η εφαπτομένη της

στο

είναι

και για να διέρχεται από την αρχή των αξόνων, θα ισχύει

άρα

αφού

επομένως

Ακόμη η

να έχει δύο άνισες πραγματικές ρίζες πρέπει κα αρκεί
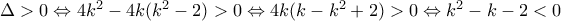
που επαληθεύεται για
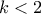
άρα
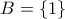
και τελικά

και

...οι πράξεις θα δείξουν...
Φιλικά και Μαθηματικά
Βασίλης
 με
με  όπου
όπου 

 είναι
είναι  τότε:
τότε:
 όπου οι πιθανότητες
όπου οι πιθανότητες 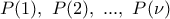 των στοιχειωδών ενδεχομένων είναι διαδοχικοί όροι γεωμετρικής προόδου με λόγο
των στοιχειωδών ενδεχομένων είναι διαδοχικοί όροι γεωμετρικής προόδου με λόγο  . Θεωρούμε τα ενδεχόμενα:
. Θεωρούμε τα ενδεχόμενα: : το
: το  τέτοιο ώστε η εφαπτομένη της
τέτοιο ώστε η εφαπτομένη της  στο
στο  να διέρχεται από την αρχή των αξόνων.
να διέρχεται από την αρχή των αξόνων. : το
: το  τέτοιο ώστε η
τέτοιο ώστε η  να έχει δύο άνισες πραγματικές ρίζες.
να έχει δύο άνισες πραγματικές ρίζες.


 άρα
άρα 
 άρα οι παρατηρήσεις κατά αύξουσα σειρά είναι
άρα οι παρατηρήσεις κατά αύξουσα σειρά είναι  τότε
τότε 
 που είναι παραγωγίσιμη με
που είναι παραγωγίσιμη με 
 και επειδή είναι
και επειδή είναι  και
και 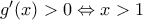 και
και  η
η  έχει ελάχιστη τιμή για
έχει ελάχιστη τιμή για  την
την 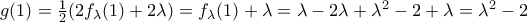

 τότε
τότε  και για την
και για την  που είναι παραγωγίσιμη με
που είναι παραγωγίσιμη με 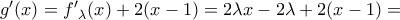
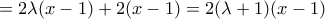 και όπως προηγούμενα έχει ελάχιστη τιμή
και όπως προηγούμενα έχει ελάχιστη τιμή  θέλουμε να είναι
θέλουμε να είναι  που είναι αδύνατη γιατί θέλουμε να είναι
που είναι αδύνατη γιατί θέλουμε να είναι 
 οπότε
οπότε 
 και ισχύει ότι
και ισχύει ότι 
 επομένως
επομένως 


 αφού
αφού  επομένως
επομένως 
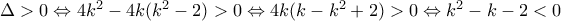
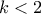 άρα
άρα 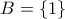 και τελικά
και τελικά  και
και 