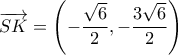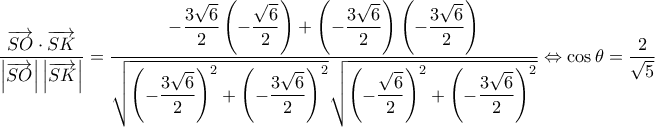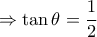Σελίδα 1 από 1
Εφαπτομένη από εφαπτόμενες
Δημοσιεύτηκε: Τρί Σεπ 23, 2025 8:47 am
από KARKAR

- Εφαπτομένη από επαφές.png (18.89 KiB) Προβλήθηκε 140 φορές
Με κέντρο σημείο

του τμήματος

γράφουμε κύκλο
. Οι εφαπτόμενες προς τον

από τα

τέμνονται στο σημείο

. Αν το

είναι σημείο της

, υπολογίστε την

.
Re: Εφαπτομένη από εφαπτόμενες
Δημοσιεύτηκε: Τετ Σεπ 24, 2025 9:44 am
από george visvikis
KARKAR έγραψε: ↑Τρί Σεπ 23, 2025 8:47 am
Εφαπτομένη από επαφές.pngΜε κέντρο σημείο

του τμήματος

γράφουμε κύκλο
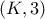
. Οι εφαπτόμενες προς τον

από τα

τέμνονται στο σημείο

. Αν το

είναι σημείο της

, υπολογίστε την

.
Θέτω
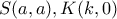
και έχω:
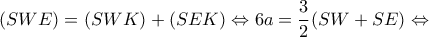
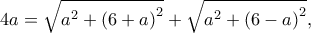
απ' όπου παίρνω
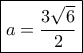


- Εφαπτομένη από εφαπτόμενες.Κ.png (20.41 KiB) Προβλήθηκε 98 φορές
Στη συνέχεια από τον τύπο
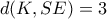
καταλήγω στην εξίσωση

Άρα,

και
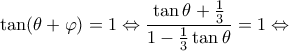
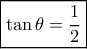
Re: Εφαπτομένη από εφαπτόμενες
Δημοσιεύτηκε: Τετ Σεπ 24, 2025 2:41 pm
από Nikitas K.
 του τμήματος
του τμήματος  γράφουμε κύκλο
γράφουμε κύκλο 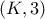 . Οι εφαπτόμενες προς τον
. Οι εφαπτόμενες προς τον 
 τέμνονται στο σημείο
τέμνονται στο σημείο  . Αν το
. Αν το  είναι σημείο της
είναι σημείο της  , υπολογίστε την
, υπολογίστε την  .
. του τμήματος
του τμήματος  γράφουμε κύκλο
γράφουμε κύκλο 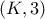 . Οι εφαπτόμενες προς τον
. Οι εφαπτόμενες προς τον 
 τέμνονται στο σημείο
τέμνονται στο σημείο  . Αν το
. Αν το  είναι σημείο της
είναι σημείο της  , υπολογίστε την
, υπολογίστε την  .
.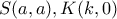 και έχω:
και έχω: 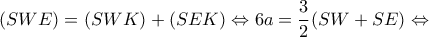
 απ' όπου παίρνω
απ' όπου παίρνω 

 καταλήγω στην εξίσωση
καταλήγω στην εξίσωση 
 και
και 
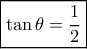
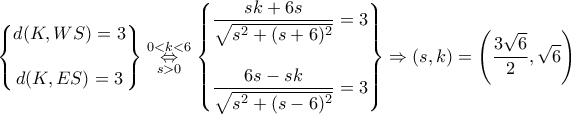
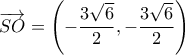 και
και