KARKAR έγραψε: ↑Τρί Ιούλ 15, 2025 10:55 pm
Στο καρτεσιανό επίπεδο είναι σχεδιασμένη η υπερβολή :

και ο κύκλος :

.
Το

είναι σημείο της υπερβολής και η

εστία της . Εξετάστε αν ο κύκλος διαμέτρου
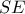
εφάπτεται του

.
Απάντηση: Ναι, εφάπτονται.
Τα κύρια βήματα γιατί οι πράξεις είναι πολλές: 'Εστω

σημείο της υπερβολής, δηλαδή ισχύει

. Η εστία της υπερβολής είναι το σημείο

όπου

. O κύκλος διαμέτρου
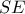
έχει μέντρο το

και ακτίνα

.
Για να αποδείξουμε ότι οι δύο κύκλοι εφάπτονται, αρκεί να δείξουμε ότι

, όπου

οι ακτίνες τους, δηλαδή να δείξουμε ότι
 (**)
(**)
Υψώνοντας στο τετράγωνο και θέτοντας

, το αποδεικτέο μετά τις πράξεις γίνεται

Πάλι στο τετράγωνο το αποδεικτέο μετά τις πράξεις γίνεται

.
Αλλά αυτή ισχύει ως ισοδύναμη μορφή της

, και η απόδειξη ολοκληρώνεται.
(**) Αυτό είναι ισοδύναμο με τον γεωμετρικό ορισμό της υπερβολής, οπότε θα μπορούσε να τέλειωνε εδώ η απόδειξη. Όμως θα το κάνω με πράξεις για λόγους αυτοδυναμίας της απόδειξης.
 και ο κύκλος :
και ο κύκλος :  .
.  είναι σημείο της υπερβολής και η
είναι σημείο της υπερβολής και η  εστία της . Εξετάστε αν ο κύκλος διαμέτρου
εστία της . Εξετάστε αν ο κύκλος διαμέτρου 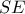 εφάπτεται του
εφάπτεται του  .
. και ο κύκλος :
και ο κύκλος :  .
.  είναι σημείο της υπερβολής και η
είναι σημείο της υπερβολής και η  εστία της . Εξετάστε αν ο κύκλος διαμέτρου
εστία της . Εξετάστε αν ο κύκλος διαμέτρου 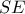 εφάπτεται του
εφάπτεται του  .
. σημείο της υπερβολής, δηλαδή ισχύει
σημείο της υπερβολής, δηλαδή ισχύει  . Η εστία της υπερβολής είναι το σημείο
. Η εστία της υπερβολής είναι το σημείο  όπου
όπου  . O κύκλος διαμέτρου
. O κύκλος διαμέτρου  και ακτίνα
και ακτίνα  .
.  , όπου
, όπου  οι ακτίνες τους, δηλαδή να δείξουμε ότι
οι ακτίνες τους, δηλαδή να δείξουμε ότι 

 .
. , και η απόδειξη ολοκληρώνεται.
, και η απόδειξη ολοκληρώνεται.