Μέγιστη τιμή αθροίσματος

#1

: Μέγιστη τιμή αθροίσματος.png (12.18 KiB) Προβλήθηκε 503 φορές

Με διάμετρο την υποτείνουσα BC=a

ορθογωνίου τριγώνου ABC

γράφω ημικύκλιο έξω απ' το τρίγωνο και

έστω

ένα μεταβλητό σημείο του ημικυκλίου. Να βρείτε τη μέγιστη τιμή του αθροίσματος MA+MB+MC

καθώς και τη θέση του

για την οποία επιτυγχάνεται.

Λάμπρος Κατσάπας · #2

george visvikis έγραψε: ↑
Τρί Ιαν 31, 2023 1:31 pm
Μέγιστη τιμή αθροίσματος.png
Με διάμετρο την υποτείνουσα ορθογωνίου τριγώνου γράφω ημικύκλιο έξω απ' το τρίγωνο και

έστω ένα μεταβλητό σημείο του ημικυκλίου. Να βρείτε τη μέγιστη τιμή του αθροίσματος

καθώς και τη θέση του για την οποία επιτυγχάνεται.

Συμβολίζω τη διάμετρο με

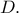Από Πτολεμαίο έχουμε:

$MA=\dfrac{b}{D}MB+\dfrac{c}{D}MC$

και επομένως αναζητούμε τη μέγιστη τιμή του αθροίσματος

$MA+MB+MC=\left ( 1+\dfrac{b}{D} \right )MB+\left ( 1+\dfrac{c}{D} \right )MC$

υπό τον περιορισμό

$MA^2+MB^2=D^2 \left ( \bigstar \right )$

Κατά τα γνωστά είναι

$\left ( 1+\dfrac{b}{D} \right )MB+\left ( 1+\dfrac{c}{D} \right )MC\leq \sqrt{\left( 1+\dfrac{b}{D} \right )^2+\left ( 1+\dfrac{c}{D} \right )^2}\sqrt{MA^2+MB^2}$

$=D\sqrt{\left( 1+\dfrac{b}{D} \right )^2+\left ( 1+\dfrac{c}{D} \right )^2}$

με την ισότητα ανν

$\dfrac{MB}{MC}=\dfrac{1+b/D}{1+c/D}.$

Από την τελευταία και την $\left ( \bigstar \right )$ βρίσκουμε στη θέση μεγιστοποίησης θα είναι

$MC=\dfrac{D}{\sqrt{1+\left ( \dfrac{1+b/D}{1+c/D} \right )^2}}.$

#3

Καλημέρα σε όλους. Επιχειρώ μια διαφορετική αντιμετώπιση με Ν. Ημιτόνων και τριγωνομετρική συνάρτηση (δίχως παραγώγους). Το κοινό σημείο με τη λύση του Λάμπρου είναι το Θεώρημα Πτολεμαίου.

: 04-02-2023 Γεωμετρία.png (19.02 KiB) Προβλήθηκε 296 φορές

Έστω $\displaystyle \widehat {MCB} = \omega ,\;\;\omega \in \left( {0,\frac{\pi }{2}} \right)$ .

Από Ν. Ημιτόνων στο MCB

είναι $\displaystyle MB = a\eta \mu \omega$ και $\displaystyle MC = a\eta \mu \left( {90^\circ - \omega } \right) = a\sigma \upsilon \nu \omega$ .

Από 1ο Θ. Πτολεμαίου $\displaystyle MA \cdot a = MB \cdot b + MC \cdot c \Leftrightarrow MA = MB \cdot \frac{b}{a} + MC \cdot \frac{c}{a}$

Οπότε $\displaystyle MA + MB + MC = \left( {a + b} \right)\eta \mu \omega + \left( {\alpha + c} \right)\sigma \upsilon \nu \omega$

Η συνάρτηση $\displaystyle f\left( \omega \right) = \left( {a + b} \right)\eta \mu \omega + \left( {\alpha + c} \right)\sigma \upsilon \nu \omega ,\;\;\omega \in \left( {0,\frac{\pi }{2}} \right)$
γράφεται $\displaystyle f\left( \omega \right) = \rho \cdot \eta \mu \left( {\omega + \varphi } \right)$ με $\displaystyle \rho = \sqrt {{{\left( {a + b} \right)}^2} + {{\left( {a + c} \right)}^2}}$ και $\displaystyle \left\{ \begin{array}{l} \sigma \upsilon \nu \varphi = \frac{{a + b}}{\rho }\\ \eta \mu \varphi = \frac{{a + c}}{\rho } \end{array} \right.$

Έχει μέγιστο όταν $\displaystyle \omega + \varphi = \frac{\pi }{2} \Rightarrow \left\{ \begin{array}{l} \eta \mu \omega = \sigma \upsilon \nu \varphi = \frac{{a + b}}{\rho }\\ \sigma \upsilon \nu \omega = \eta \mu \varphi = \frac{{a + c}}{\rho } \end{array} \right.$

Τότε $\displaystyle MB = a\eta \mu \omega = a \cdot \frac{{a + b}}{\rho },\;\;MC = a\sigma \upsilon \nu \omega = a \cdot \frac{{a + c}}{\rho }$ και $\displaystyle MA = b \cdot \frac{{a + b}}{\rho } + c \cdot \frac{{a + c}}{\rho } = \frac{{ab + ac + {a^2}}}{\rho }$

Η μέγιστη τιμή του αθροίσματος είναι ίση με $\displaystyle f\left( {\frac{\pi }{2} - \varphi } \right) = \rho$ .

#4

Αφού ευχαριστήσω το Λάμπρο και το Γιώργο για τις πολύ ωραίες λύσεις τους, να πω ότι η άσκηση είναι

από το βιβλίο Geometric Problems on Maxima and Minima των Andreescu & MushKarov &Stoyanov

Μέγιστη τιμή αθροίσματος

Μέγιστη τιμή αθροίσματος

Re: Μέγιστη τιμή αθροίσματος

Re: Μέγιστη τιμή αθροίσματος

Re: Μέγιστη τιμή αθροίσματος

Μέλη σε σύνδεση