Εμβαδόν ισοπλεύρου τριγώνου

KARKAR · #1

: Εμβαδόν ισοπλεύρου τριγώνου.png (17.5 KiB) Προβλήθηκε 528 φορές

Οι τρεις ομόκεντροι κύκλοι , έχουν ακτίνες 1 , 2

και

. Καταφέραμε να σχεδιάσουμε ισόπλευρο

τρίγωνο SPT

, με μία κορυφή σε κάθε κύκλο . Πόσο είναι το εμβαδόν αυτού του τριγώνου ;

#2

KARKAR έγραψε: ↑
Πέμ Δεκ 08, 2022 1:00 pm
Εμβαδόν ισοπλεύρου τριγώνου.pngΟι τρεις ομόκεντροι κύκλοι , έχουν ακτίνες και . Καταφέραμε να σχεδιάσουμε ισόπλευρο

τρίγωνο , με μία κορυφή σε κάθε κύκλο . Πόσο είναι το εμβαδόν αυτού του τριγώνου ;

Κατασκευή: Παίρνω στον εξωτερικό κύκλο χορδή AT=3.

Το

είναι προφανώς ισόπλευρο. Η

τέμνει

τον μεσαίο κύκλο στο

Τέλος, το ισόπλευρο πλευράς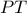

τέμνει τον εσωτερικό κύκλο στο

και είναι το ζητούμενο.

: Εμβαδόν ισοπλεύρου.Κ.png (20.62 KiB) Προβλήθηκε 496 φορές

$\displaystyle {x^2} = A{P^2} + A{T^2} - AP \cdot AT = 7 \Rightarrow$ $\boxed{(PST) = \frac{{{x^2}\sqrt 3 }}{4} = \frac{{7\sqrt 3 }}{4}}$

ΥΓ. Η κατασκευή αυτή δεν είναι η κλασική, αλλά ταιριάζει με τους δοσμένους κύκλους.

KARKAR · #3

: ισοπλ.png (17.83 KiB) Προβλήθηκε 471 φορές

Γιώργο , η λύση σου πιθανόν να αφήνει την απορία , πώς είμαστε βέβαιοι ότι το

θα βρεθεί πάνω

στον μικρό κύκλο . Αν λοιπόν θεωρήσουμε $OS \parallel AT$ , τότε με νόμο συνημιτόνων ( στα τρίγωνα

POS

και

) , προκύπτει : $SP=ST=\sqrt{7}=PT$ .

#4

KARKAR έγραψε: ↑
Πέμ Δεκ 08, 2022 6:21 pm
ισοπλ.pngΓιώργο , η λύση σου πιθανόν να αφήνει την απορία , πώς είμαστε βέβαιοι ότι το θα βρεθεί πάνω

στον μικρό κύκλο .

Θανάση, το έκανα με Πτολεμαίο στο εγγράψιμο OSTP.

$\displaystyle 2x + OS \cdot x = 3x \Leftrightarrow$ $\boxed{OS=1}$ και το

είναι σημείο του εσωτερικού κύκλου.

#5

KARKAR έγραψε: ↑
Πέμ Δεκ 08, 2022 1:00 pm
Εμβαδόν ισοπλεύρου τριγώνου.pngΟι τρεις ομόκεντροι κύκλοι , έχουν ακτίνες και . Καταφέραμε να σχεδιάσουμε ισόπλευρο

τρίγωνο , με μία κορυφή σε κάθε κύκλο . Πόσο είναι το εμβαδόν αυτού του τριγώνου ;

Σε κάποιο σημείο

του μεσαίου κύκλου φέρνω την εφαπτομένη ευθεία $\left( \varepsilon \right)$ . Η ευθεία

τέμνει τον μικρό κύκλο στο

και το μεγάλο στο

.

Στρέφω την $\left( \varepsilon \right)$ γύρω από το

κατά γωνία $\theta = 60^\circ$ . Η ευθεία που προκύπτει διέρχεται από το

και τέμνει ακόμα τον μικρό κύκλο στο

.

: Εμβαδόν ισοσπλεύρου τριγώνου_Επιτυχής με στροφή.png (26.38 KiB) Προβλήθηκε 425 φορές

Κατασκευάζω τώρα το ισόπλευρο τρίγωνο με πλευρά την

( με αυτό τον προσανατολισμό) .

Η τρίτη κορυφή του

ανήκει στον πιο μεγάλο κύκλο .

Επειδή $\vartriangle OAS \to \left( {120^\circ ,30^\circ ,30^\circ } \right)$ θα είναι : $P{S^2} = {2^2} + {1^2} + 2 \cdot 2 \cdot \dfrac{1}{2} = 7$ , άρα $\boxed{\left( {PST} \right) = \frac{{P{S^2}\sqrt 3 }}{4} = \frac{{7\sqrt 3 }}{4}}$ .

Υπάρχουν πολλοί άλλοι τρόποι κατασκευής .

#6

KARKAR έγραψε: ↑
Πέμ Δεκ 08, 2022 1:00 pm
Εμβαδόν ισοπλεύρου τριγώνου.pngΟι τρεις ομόκεντροι κύκλοι , έχουν ακτίνες και . Καταφέραμε να σχεδιάσουμε ισόπλευρο

τρίγωνο , με μία κορυφή σε κάθε κύκλο . Πόσο είναι το εμβαδόν αυτού του τριγώνου ;

Σε σημείο

του μικρότερου κύκλου φέρνω εφαπτομένη και τέμνει το μεσαίο στα $F\,\,\kappa \alpha \iota \,\,P$ .

Ας πούμε

το σημείο τομής της

με το μεγάλο κύκλο . Προφανές ότι , $\widehat {{a_1}} = \widehat {{a_2}} = 60^\circ$ .

Επίσης με εφαρμογή του Π. Θ. στα $\vartriangle MPO\,\,\kappa \alpha \iota \,\,\vartriangle MTP$ έχω:

$T{P^2} = T{M^2} + M{P^2} = T{M^2} + O{P^2} - O{M^2} = 4 + 4 - 1 = 7$ και άρα $TP = TF = \sqrt 7 \,\,\left( 1 \right)$

: Εμβαδόν ισοσπλέυρου τριγώνου_new.png (27.67 KiB) Προβλήθηκε 396 φορές

Φέρνω την

και τέμνει τον μικρό κύκλο στο

.

Με Θ. συνημίτονου στα $\vartriangle OSP\,\,\kappa \alpha \iota \,\,\vartriangle OST$ έχω : $\left\{ \begin{gathered} S{P^2} = {2^2} + {1^2} - 2 \cdot 2 \cdot 1 \cdot \left( { - \frac{1}{2}} \right) = 7 \hfill \\ T{S^2} = {3^2} + {1^2} - 2 \cdot 3 \cdot 1 \cdot \frac{1}{2} = 7 \hfill \\ \end{gathered} \right.$

Λόγω της $\left( 1 \right)$ και των προηγουμένων είναι: $\boxed{SP = PT = TS = \sqrt 7 \,\,\kappa \alpha \iota \,\,\left( {STP} \right) = \frac{{7\sqrt 3 }}{4}}$

nickchalkida · #7

Ανάλυση, κατασκευή: Με σταθερό το

, περιστρέφοντας το

και

την τρίτη πλευρά του ισοπλεύρου SPT

είναι

$\left\{ S=ct \right.$ , το

διαγράφει κύκλο, $\left.\displaystyle {PM \over MS}=1 \right\}$ $\rightarrow$ Το

διαγράφει κύκλο (K,KL)

$\left\{ S=ct \right.$ , το

διαγράφει κύκλο, $\left.\displaystyle {TS \over SP}=1, T\widehat{S}P=ct\right\}$ $\rightarrow$ Το

διαγράφει κύκλο (D,DB)

Τα κέντρα και οι ακτίνες των κύκλων (K,KL), (D,DB)

προσδιορίζονται από τις οριακές θέσεις του

στα

,

.
Το ζητούμενο ισόπλευρο προσδιορίζεται από την τομή του κύκλου (D,DB)

με τον αρχικό εξωτερικό.
[στο συγκεκριμένο πρόβλημα εφάπτεται.] Οι μετρικές αφήνονται για τον σχολαστικό αναγνώστη.

Εμβαδόν ισοπλεύρου τριγώνου

Εμβαδόν ισοπλεύρου τριγώνου

Re: Εμβαδόν ισοπλεύρου τριγώνου

Re: Εμβαδόν ισοπλεύρου τριγώνου

Re: Εμβαδόν ισοπλεύρου τριγώνου

Re: Εμβαδόν ισοπλεύρου τριγώνου

Re: Εμβαδόν ισοπλεύρου τριγώνου

Re: Εμβαδόν ισοπλεύρου τριγώνου

Μέλη σε σύνδεση