
- max.png (99.43 KiB) Προβλήθηκε 180 φορές
Μια γεωμετρική προσέγγιση...
Έστω τμήμα
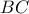
,

, το μέσο του
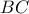
και

σταθερό σημείο του

.
Θεωρούμε σημείο

να κινείται στην κάθετο στην
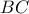
στο

.
.........................................................................................
Αν

,

τα ύψη του τριγώνου

τότε η ευθεία

τέμνει την ευθεία
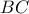
σε σημείο
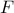
, το οποίο είναι σταθερό, ανεξάρτητο από τη θέση του

.
Πράγματι, από την ομοιότητα των τριγώνων

και με τη βοήθεια των κύκλων

, έχουμε
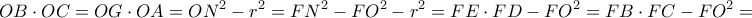

Από σημείο

το οποίο κινείται στο
φέρουμε

...............................................................................................
Από το

φέρουμε παράλληλη στην

η οποία τέμνει το

στο σημείο
.
Θα δείξουμε ότι το τετράπλευρο

είναι παραλληλόγραμμο.
Πράγματι

. Άρα

οπότε

.
..................................................................................................
Έτσι δείξαμε ότι: Θεωρώντας το σημείο

σε μια τυχαία θέση πάνω στην κάθετο στην
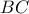
στο

και το σημείο

να κινείται στο
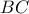
,
η κορυφή
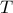
του παραλληλογράμμου

κινείται στο τμήμα

της ευθείας,
η οποία περνάει από το σταθερό σημείο
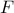
της ευθείας
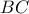
.
.................................................................................................
Ακόμη για το εμβαδόν του παραλληλογράμμου είναι:
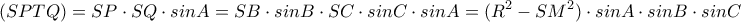
.
Άρα

.
Οπότε η μέγιστη τιμή του εμβαδού

είναι

όταν το

περνάει από το μέσο του

.
 του τριγώνου
του τριγώνου  κινείται στον ημιάξονα
κινείται στον ημιάξονα  . Σημείο
. Σημείο  κινείται στη βάση
κινείται στη βάση  .
. και συμπληρώνω το παραλληλόγραμμο
και συμπληρώνω το παραλληλόγραμμο  .
. είναι τμήμα ευθείας , η οποία διέρχεται από σταθερό σημείο .
είναι τμήμα ευθείας , η οποία διέρχεται από σταθερό σημείο . , για ποια θέση του
, για ποια θέση του  μεγιστοποιείται το :
μεγιστοποιείται το : 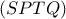 ;
;
 ,
,  , το μέσο του
, το μέσο του  σταθερό σημείο του
σταθερό σημείο του  .
. να κινείται στην κάθετο στην
να κινείται στην κάθετο στην  ,
,  τα ύψη του τριγώνου
τα ύψη του τριγώνου  τότε η ευθεία
τότε η ευθεία 
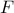 , το οποίο είναι σταθερό, ανεξάρτητο από τη θέση του
, το οποίο είναι σταθερό, ανεξάρτητο από τη θέση του  και με τη βοήθεια των κύκλων
και με τη βοήθεια των κύκλων  , έχουμε
, έχουμε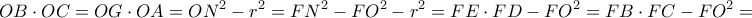

 το οποίο κινείται στο
το οποίο κινείται στο 
 φέρουμε παράλληλη στην
φέρουμε παράλληλη στην  η οποία τέμνει το
η οποία τέμνει το 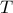 .
. είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. . Άρα
. Άρα  οπότε
οπότε  .
.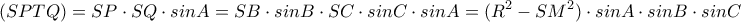 .
. .
. είναι
είναι 
 περνάει από το μέσο του
περνάει από το μέσο του  .
.
