KARKAR έγραψε: ↑Κυρ Οκτ 23, 2022 7:56 pm
Στο καρτεσιανό επίπεδο θεωρούμε το σημείο

. ( Εφαρμογή :
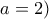
Σημείο

κινείται στην ευθεία

και σημείο

στην

, ώστε :

.
Δείξτε ότι ο γεωμετρικός τόπος του βαρυκέντρου του τριγώνου

είναι παραβολή και
υπολογίστε το

, ώστε η κορυφή της παραβολής να συμπίπτει με την αρχή των αξόνων .

- barycenter.png (110.76 KiB) Προβλήθηκε 232 φορές
Παρόμοια με
την απάντηση του κ. Νίκου εδώ.
Οι συντεταγμένες των σημείων φαίνονται στο σχήμα. Αφού

, πρέπει το γινόμενο των εφαπτομένων των φορέων τους να είναι

:
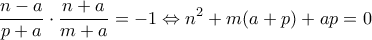
Τώρα, για τα σημεία του γεωμετρικού τόπου ισχύει:

Συνδυάζοντας τα παραπάνω, παίρνω:
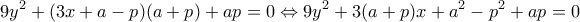
που είναι παραβολή της μορφής
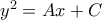
, άρα η κορυφή της βρίσκεται στον άξονα

.
Τώρα, επειδή το

ανήκει στην παραβολή, θα είναι και η κορυφή της. Για

, η παραπάνω σχέση γράφεται:
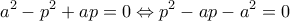
Λύνω τη δευτεροβάθμια ως προς

: έχει ρίζες για κάθε

τις
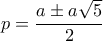
και επειδή
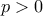
, υποχρεωτικά:

 . ( Εφαρμογή :
. ( Εφαρμογή : 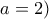
 κινείται στην ευθεία
κινείται στην ευθεία  και σημείο
και σημείο  στην
στην  , ώστε :
, ώστε :  .
. είναι παραβολή και
είναι παραβολή και  , ώστε η κορυφή της παραβολής να συμπίπτει με την αρχή των αξόνων .
, ώστε η κορυφή της παραβολής να συμπίπτει με την αρχή των αξόνων .
 , πρέπει το γινόμενο των εφαπτομένων των φορέων τους να είναι
, πρέπει το γινόμενο των εφαπτομένων των φορέων τους να είναι  :
: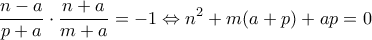

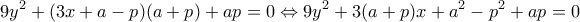
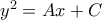 , άρα η κορυφή της βρίσκεται στον άξονα
, άρα η κορυφή της βρίσκεται στον άξονα  .
. ανήκει στην παραβολή, θα είναι και η κορυφή της. Για
ανήκει στην παραβολή, θα είναι και η κορυφή της. Για  , η παραπάνω σχέση γράφεται:
, η παραπάνω σχέση γράφεται: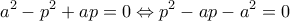
 τις
τις 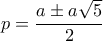 και επειδή
και επειδή 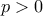 , υποχρεωτικά:
, υποχρεωτικά: