 ο καθένας .
ο καθένας .Το
 είναι κοινό εξωτερικά εφαπτόμενο τμήμα .
είναι κοινό εξωτερικά εφαπτόμενο τμήμα .Υπολογίστε το μέγιστο εμβαδόν του τραπεζίου
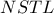 .
. ο καθένας .
ο καθένας . είναι κοινό εξωτερικά εφαπτόμενο τμήμα .
είναι κοινό εξωτερικά εφαπτόμενο τμήμα .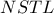 .
.
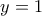 , οπότε
, οπότε  .
. σημείο του
σημείο του  . Είναι
. Είναι 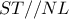 , οπότε όταν
, οπότε όταν 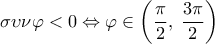 έχουμε ισοσκελές τραπέζιο, όπως ζητά η εκφώνηση, ενώ αν ήταν
έχουμε ισοσκελές τραπέζιο, όπως ζητά η εκφώνηση, ενώ αν ήταν ![\displaystyle \varphi \in \left[ {0,\;\frac{\pi }{2}} \right) \cup \left[ {\frac{{3\pi }}{2},\;2\pi } \right] \displaystyle \varphi \in \left[ {0,\;\frac{\pi }{2}} \right) \cup \left[ {\frac{{3\pi }}{2},\;2\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/50a7fbf26302dfe4aad99446d67c93e9.png) θα είχαμε παραλληλόγραμμο.
θα είχαμε παραλληλόγραμμο. , όπου
, όπου 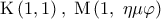 .
.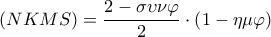 .
. έχει παράγωγο
έχει παράγωγο 
 (με λογισμικό).
(με λογισμικό). , βρίσκουμε το εμβαδόν του μισού τραπεζίου
, βρίσκουμε το εμβαδόν του μισού τραπεζίου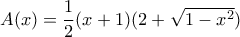 , δηλαδή :
, δηλαδή :  .
.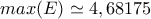 για :
για : 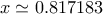
Βρίσκω
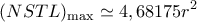 όταν
όταν  Βλέπω ότι ο Θανάσης έγραψε ήδη το αποτέλεσμα. Δυο λόγια για τη λύση.
Βλέπω ότι ο Θανάσης έγραψε ήδη το αποτέλεσμα. Δυο λόγια για τη λύση. τότε
τότε  και
και 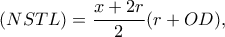 όπου
όπου 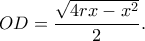

![\boxed{x = ST = \frac{r}{3}\left( {2 + \sqrt[3]{{62 - 3\sqrt {183} }} + \sqrt[3]{{62 + 3\sqrt {183} }}} \right)} \boxed{x = ST = \frac{r}{3}\left( {2 + \sqrt[3]{{62 - 3\sqrt {183} }} + \sqrt[3]{{62 + 3\sqrt {183} }}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/3c115fe9cefa4538590270261c545bf4.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες