Το
 κινείται στην πλευρά
κινείται στην πλευρά  τετραγώνου
τετραγώνου  πλευράς
πλευράς  και κέντρου
και κέντρου 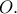 Αν η
Αν η  τέμνει την
τέμνει την  στο
στο  και
και η
 την
την  στο
στο  να δείξετε ότι το γινόμενο
να δείξετε ότι το γινόμενο  είναι σταθερό, ανεξάρτητο της επιλογής του σημείου
είναι σταθερό, ανεξάρτητο της επιλογής του σημείου 
 κινείται στην πλευρά
κινείται στην πλευρά  τετραγώνου
τετραγώνου  πλευράς
πλευράς  και κέντρου
και κέντρου 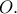 Αν η
Αν η  τέμνει την
τέμνει την  στο
στο  και
και  την
την  στο
στο  να δείξετε ότι το γινόμενο
να δείξετε ότι το γινόμενο  είναι σταθερό, ανεξάρτητο της επιλογής του σημείου
είναι σταθερό, ανεξάρτητο της επιλογής του σημείου 
 Θεωρούμε το μη κυρτό τετράπλευρο
Θεωρούμε το μη κυρτό τετράπλευρο 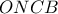 ως το εκφυλισμένο εξάγωνο
ως το εκφυλισμένο εξάγωνο 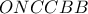 και παρατηρούμε ότι τα σημεία
και παρατηρούμε ότι τα σημεία  και
και 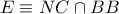 και
και 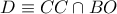 είναι συνευθειακά.
είναι συνευθειακά. είναι ομοκυκλικά.
είναι ομοκυκλικά. δηλαδή, ανήκει στον περίκυκλο έστω
δηλαδή, ανήκει στον περίκυκλο έστω  του τριγώνου
του τριγώνου  και άρα, ισχύει
και άρα, ισχύει  Από
Από  και
και 

 προκύπτει ότι η ευθεία
προκύπτει ότι η ευθεία  εφάπτεται του περίκυκλου έστω
εφάπτεται του περίκυκλου έστω  του μεταβλητού τριγώνου
του μεταβλητού τριγώνου  στο σημείο
στο σημείο  .
. και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. ως τομή της
ως τομή της  με τον κύκλο των
με τον κύκλο των  (διαμέτρου
(διαμέτρου  ). Η
). Η  τέμνει την
τέμνει την  στο
στο  .
. 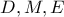 είναι συνευθειακά.
είναι συνευθειακά. είναι όμοια, ενώ η
είναι όμοια, ενώ η  διχοτόμος της ορθής
διχοτόμος της ορθής  αφού
αφού  .
. .
.  είναι όμοια με
είναι όμοια με  .
.  είναι συνευθειακά άρα και τα
είναι συνευθειακά άρα και τα 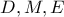 συνευθειακά επίσης.
συνευθειακά επίσης.Ανgeorge visvikis έγραψε: ↑Παρ Δεκ 03, 2021 6:52 pmΣταθερό γινόμενο 2.png
Τοκινείται στην πλευρά
τετραγώνου
πλευράς
και κέντρου
Αν η
τέμνει την
στο
και
ητην
στο
να δείξετε ότι το γινόμενο
είναι σταθερό, ανεξάρτητο της επιλογής του σημείου

 είναι η τομή των
είναι η τομή των  και
και  η τομή των
η τομή των  τότε, λόγω της "συντρεχουσότητας" στο
τότε, λόγω της "συντρεχουσότητας" στο  και του θεωρήματος Desarges και επειδή οι
και του θεωρήματος Desarges και επειδή οι 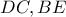 είναι παράλληλες η
είναι παράλληλες η  θα περνά από το "επ΄ άπειρο σημείο τομής" των
θα περνά από το "επ΄ άπειρο σημείο τομής" των 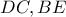 οπότε θα είναι παράλληλη τους. Έτσι το
οπότε θα είναι παράλληλη τους. Έτσι το  καθίσταται ορθόκεντρο του τριγώνου
καθίσταται ορθόκεντρο του τριγώνου  , άρα η
, άρα η  είναι κάθετη στην
είναι κάθετη στην  Άρα τα σημεία
Άρα τα σημεία  είναι ομοκυκλικά κύκλου με διάμετρο
είναι ομοκυκλικά κύκλου με διάμετρο  κέντρου έστω
κέντρου έστω 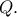 Αν
Αν  το αντιδιαμετρικό του
το αντιδιαμετρικό του  , τότε εύκολα παίρνουμε ότι το ζητούμενο γινόμενο μας ισούται με το σταθερό
, τότε εύκολα παίρνουμε ότι το ζητούμενο γινόμενο μας ισούται με το σταθερό 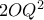 .
.Θεωρούμε σημείοgeorge visvikis έγραψε: ↑Παρ Δεκ 03, 2021 6:52 pmΣταθερό γινόμενο 2.png
Τοκινείται στην πλευρά
τετραγώνου
πλευράς
και κέντρου
Αν η
τέμνει την
στο
και
ητην
στο
να δείξετε ότι το γινόμενο
είναι σταθερό, ανεξάρτητο της επιλογής του σημείου

 στην
στην  ώστε
ώστε 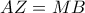 οπότε και
οπότε και  άρα
άρα 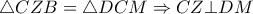
 ορθόκεντρο του
ορθόκεντρο του 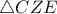 .Επιπλέον,λόγω της προφανούς ισότητας των τριγώνων
.Επιπλέον,λόγω της προφανούς ισότητας των τριγώνων  οι γωνίες
οι γωνίες 
 ,άρα
,άρα 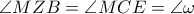
 εγγράψιμμο και
εγγράψιμμο και σταθερό
σταθερόΜιας και μαζεύτηκε εδώ η ωραία γεωμετρική παρέα, ας πω και εγώ την άποψη μου για την εγγραψιμότητα φυσικά του εν λόγω τετραπλεύρου. Ανgeorge visvikis έγραψε: ↑Παρ Δεκ 03, 2021 6:52 pmΣταθερό γινόμενο 2.png
Τοκινείται στην πλευρά
τετραγώνου
πλευράς
και κέντρου
Αν η
τέμνει την
στο
και
ητην
στο
να δείξετε ότι το γινόμενο
είναι σταθερό, ανεξάρτητο της επιλογής του σημείου

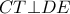 τότε προφανώς τα τετράπλευρα
τότε προφανώς τα τετράπλευρα  είναι εγγράψιμα σε κύκλους διαμέτρων
είναι εγγράψιμα σε κύκλους διαμέτρων  αντίστοιχα. Άρα
αντίστοιχα. Άρα 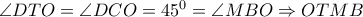 εγγράψιμο οπότε:
εγγράψιμο οπότε:  και συνεπώς τα
και συνεπώς τα  είναι ομοκυκλικά.
είναι ομοκυκλικά.Ας είναιgeorge visvikis έγραψε: ↑Παρ Δεκ 03, 2021 6:52 pmΣταθερό γινόμενο 2.png
Τοκινείται στην πλευρά
τετραγώνου
πλευράς
και κέντρου
Αν η
τέμνει την
στο
και
ητην
στο
να δείξετε ότι το γινόμενο
είναι σταθερό, ανεξάρτητο της επιλογής του σημείου

 η προβολή του
η προβολή του  στην
στην  . Θέτω :
. Θέτω :  .
. θα ισχύουν ταυτόχρονα:
θα ισχύουν ταυτόχρονα: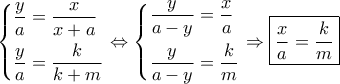 .
. 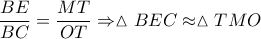 ( ορθογώνια με κάθετες πλευρές ανάλογες)
( ορθογώνια με κάθετες πλευρές ανάλογες) οπότε το τετράπλευρο
οπότε το τετράπλευρο 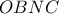 είναι εγράψιμο άρα ,
είναι εγράψιμο άρα ,  . Έστω ότι η
. Έστω ότι η 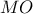 τέμνει την
τέμνει την  στο
στο  , άρα
, άρα 
 εξασφαλίζει ότι τα σημεία
εξασφαλίζει ότι τα σημεία 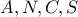 είναι ομοκυκλικά και άρα λόγω της
είναι ομοκυκλικά και άρα λόγω της  έχω:
έχω: 
Για την όμορφη λύση του φίλτατου Σωτήρη, δώρο το σχήμα έτσι ώστε να εμφανίζεται ολόκληρο στην προεπισκόπηση εκτύπωσης.S.E.Louridas έγραψε: ↑Σάβ Δεκ 04, 2021 6:41 pmΑνείναι η τομή των
και
η τομή των
τότε, λόγω της "συντρεχουσότητας" στο
και του θεωρήματος Desarges και επειδή οι
είναι παράλληλες η
θα περνά από το "επ΄ άπειρο σημείο τομής" των
οπότε θα είναι παράλληλη τους. Έτσι το
καθίσταται ορθόκεντρο του τριγώνου
, άρα η
είναι κάθετη στην
Άρα τα σημεία
είναι ομοκυκλικά κύκλου με διάμετρο
κέντρου έστω
Αν
το αντιδιαμετρικό του
, τότε εύκολα παίρνουμε ότι το ζητούμενο γινόμενο μας ισούται με το σταθερό
.
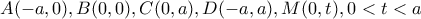 , οπότε,
, οπότε,  η τομή των
η τομή των  .
.


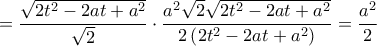 , σταθερό.
, σταθερό.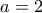 οι εξισώσεις γίνονται απλούστερες, το γινόμενο προκύπτει σταθερό, αλλά δεν είναι εμφανές στο αποτέλεσμα το
οι εξισώσεις γίνονται απλούστερες, το γινόμενο προκύπτει σταθερό, αλλά δεν είναι εμφανές στο αποτέλεσμα το  .
.

 κι επειδή
κι επειδή  τα τρίγωνα
τα τρίγωνα 
 είναι όμοια. Οπότε
είναι όμοια. Οπότε  δηλαδή η
δηλαδή η  εφάπτεται στον περίκυκλο του τριγώνου
εφάπτεται στον περίκυκλο του τριγώνου  και
και 


 που αποδεικνύει το ζητούμενο.
που αποδεικνύει το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες