 μέχρι το
μέχρι το  έτσι, ώστε το άθροισμα των αριθμών σε οποιοδήποτε σχήμα της μορφής (βλ. σχήμα) να διαιρείται με το
έτσι, ώστε το άθροισμα των αριθμών σε οποιοδήποτε σχήμα της μορφής (βλ. σχήμα) να διαιρείται με το  ;
; μέχρι το
μέχρι το  έτσι, ώστε το άθροισμα των αριθμών σε οποιοδήποτε σχήμα της μορφής (βλ. σχήμα) να διαιρείται με το
έτσι, ώστε το άθροισμα των αριθμών σε οποιοδήποτε σχήμα της μορφής (βλ. σχήμα) να διαιρείται με το  ;
;

Μπορείτε να το εξηγήσετε αυτό το σημείο λίγο παραπάνω; Γιατί σε κάθε "τριάδα" πρέπει να χρησιμοποιήσουμε πολλαπλάσιο του
 ; Για παράδειγμα θα μπορούσαμε να έχουμε την "τριάδα" με τους αριθμούς
; Για παράδειγμα θα μπορούσαμε να έχουμε την "τριάδα" με τους αριθμούς  με άθροισμα
με άθροισμα  πολλαπλάσιο του
πολλαπλάσιο του  , αλλά αναμεσά τους δεν υπάρχει κανένα πολλαπλάσιο του
, αλλά αναμεσά τους δεν υπάρχει κανένα πολλαπλάσιο του  .
. Επιτρέπεται, ναι.
Ο τρόπος με τον οποίο μου λέτε ότι κάνω λάθος είναι λάθος! και λυπάμαι που ασχολήθηκα!Al.Koutsouridis έγραψε: ↑Τετ Σεπ 29, 2021 11:28 pmΜπορείτε να το εξηγήσετε αυτό το σημείο λίγο παραπάνω; Γιατί σε κάθε "τριάδα" πρέπει να χρησιμοποιήσουμε πολλαπλάσιο του; Για παράδειγμα θα μπορούσαμε να έχουμε την "τριάδα" με τους αριθμούς
με άθροισμα
πολλαπλάσιο του
, αλλά αναμεσά τους δεν υπάρχει κανένα πολλαπλάσιο του
.
Επιτρέπεται, ναι.


 , δεν τεκμαίρεται. Όπως γράφει ο θεματοθέτης, πώς αποκλείεις μία τετράδα να περιέχει για παράδειγμα τους αριθμούς
, δεν τεκμαίρεται. Όπως γράφει ο θεματοθέτης, πώς αποκλείεις μία τετράδα να περιέχει για παράδειγμα τους αριθμούς  οι οποίοι έχουν άθροισμα κάποιο πολλαπλάσιο του
οι οποίοι έχουν άθροισμα κάποιο πολλαπλάσιο του  , πλην όμως κανένας από τους προσθετέους δεν είναι πολλαπλάσιο του
, πλην όμως κανένας από τους προσθετέους δεν είναι πολλαπλάσιο του  ; Ανάλογα παραδείγματα υπάρχουν πάμπολλα, π.χ. γιατί αποκλείεται η τετράδα
; Ανάλογα παραδείγματα υπάρχουν πάμπολλα, π.χ. γιατί αποκλείεται η τετράδα  με άθροισμα
με άθροισμα  αλλά χωρίς να περιέχει πολλαπλάσιο του
αλλά χωρίς να περιέχει πολλαπλάσιο του  ;
;

abgd έγραψε: ↑Πέμ Σεπ 30, 2021 11:44 amΚύριε Λάμπρου και βέβαια έχει δίκιο ο θεματοθέτης Αλ. Κατσουρίδης για την ένστασή του.
Δεν ισχυρίστηκα ποτέ ότι ότι σε κάθε τετράδα πρέπει να χρησιμοποιηθεί ένα πολλαπλάσιο του 5, Προφανώς σε μια τετράδα πρέπει να χρησιμοποιήσουμε 2 ή 4 πολλαπλάσια του 5.
Ο κ. Κατσουρίδης όμως ζητώντας μου να "εξηγήσω λίγο παραπάνω" το προφανώς ανεξήγητο, το κάνει με ειρωνική διάθεση και λυπάμαι για αυτό, όπως και για το λάθος μου το οποίο δεν ήταν "τυπογραφικό": εντελώς απρόσεκτα θεώρησα ότι στο σχήμα έχουμε τρεις αριθμούς.
Να ζητήσω πάλι συγνώμη για την τόση αναστάτωση.
Σας υπόσχομαι ότι δεν θα το ξανακάνω!
Πλην όμως στο αρχικό σου ποστ γράφεις
Με άλλα λόγια, υποθέτεις ότι σε κάθε τριάδα (ή τετράδα, αν πρόκειται για σφάλμα εκ παραδρομής) πρέπει να υπάρχουν πολλαπλάσια του
 . Δεν τεκμηριώθηκε ο ισχυρισμός, αλλά σε αυτό βασίστηκε η λύση σου που λέει ότι έχουμε
. Δεν τεκμηριώθηκε ο ισχυρισμός, αλλά σε αυτό βασίστηκε η λύση σου που λέει ότι έχουμε 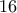 τετράδες (όπως άλλωστε τις σχεδίασες) αλλά μόνο
τετράδες (όπως άλλωστε τις σχεδίασες) αλλά μόνο  πεντάρια.
πεντάρια.Aπάντηση: Δεν μπορούμε.Al.Koutsouridis έγραψε: ↑Κυρ Σεπ 26, 2021 11:13 amΜπορούμε άραγε να τοποθετήσουμε στα κελιά μιας σκακιέρας τους αριθμούς από τομέχρι το
έτσι, ώστε το άθροισμα των αριθμών σε οποιοδήποτε σχήμα της μορφής (βλ. σχήμα) να διαιρείται με το
;
 πολλαπλάσιο του
πολλαπλάσιο του  και
και  πολλαπλάσιο του
πολλαπλάσιο του  . Αφαιρούμε κατά μέλη, οπότε
. Αφαιρούμε κατά μέλη, οπότε  πολλαπλάσιο του
πολλαπλάσιο του  , δηλαδή τα
, δηλαδή τα  και
και  αφήνουν το ίδιο υπόλοιπο μόντουλο
αφήνουν το ίδιο υπόλοιπο μόντουλο  . Αυτό είναι το κλειδί.
. Αυτό είναι το κλειδί.  .
.  τον αριθμό. Μα στους αριθμούς
τον αριθμό. Μα στους αριθμούς  έως
έως  δεν υπάρχουν
δεν υπάρχουν  αριθμοί με το ίδιο μόντουλο. Π.χ. οι
αριθμοί με το ίδιο μόντουλο. Π.χ. οι  είναι
είναι  τον αριθμό. Όμοια οι υπόλοιπες περιπτώσεις. Άτοπο και τελειώσαμε.
τον αριθμό. Όμοια οι υπόλοιπες περιπτώσεις. Άτοπο και τελειώσαμε. δύο θετικοί ακέραιοι με
δύο θετικοί ακέραιοι με  ή
ή  .
. της μορφής
όπου τοποθετούμε, σε κάθε κελί έναν θετικό ακέραιο.
της μορφής
όπου τοποθετούμε, σε κάθε κελί έναν θετικό ακέραιο. 
 είναι πολλαπλάσιο του 5 αν και μόνο αν
είναι πολλαπλάσιο του 5 αν και μόνο αν  είναι πολλαπλάσιο του 5,
είναι πολλαπλάσιο του 5, 
 , στην ορθογώνια διάταξη
, στην ορθογώνια διάταξη  , έτσι ώστε να ισχύει η συνθήκη του προβλήματος
, έτσι ώστε να ισχύει η συνθήκη του προβλήματος 
 όπου τοποθετούμε τους αριθμούς
όπου τοποθετούμε τους αριθμούς  όπως φαίνεται στο παρακάτω σχήμα.
Οι αριθμοί αυτοί ανήκουν στο σύνολο
όπως φαίνεται στο παρακάτω σχήμα.
Οι αριθμοί αυτοί ανήκουν στο σύνολο  και παρατηρούμε ότι η διαφορά δύο εξ αυτών είναι πολλαπλάσιο του 5 αν και μόνο αν οι αριθμοί είναι ίσοι μεταξύ τους.
και παρατηρούμε ότι η διαφορά δύο εξ αυτών είναι πολλαπλάσιο του 5 αν και μόνο αν οι αριθμοί είναι ίσοι μεταξύ τους.












Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες