 , τέμνει τον κύκλο :
, τέμνει τον κύκλο :  στα σημεία
στα σημεία 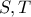 . Αν
. Αν  είναι
είναιοι προβολές των
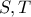 στον άξονα
στον άξονα  , υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου
, υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου  .
. , τέμνει τον κύκλο :
, τέμνει τον κύκλο :  στα σημεία
στα σημεία 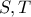 . Αν
. Αν  είναι
είναι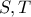 στον άξονα
στον άξονα  , υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου
, υπολογίστε το μέγιστο εμβαδόν του τετραπλεύρου  .
.Ας είναι
 και
και 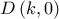 το σημείο τομής της ευθείας που δόθηκε με τον κατακόρυφο άξονα.
το σημείο τομής της ευθείας που δόθηκε με τον κατακόρυφο άξονα. . Από το σύστημα:
. Από το σύστημα:  .
. και δεδομένου ότι
και δεδομένου ότι  προκύπτει:
προκύπτει: , όπου
, όπου 
 και είναι :
και είναι :  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες