 έχει τις κορυφές
έχει τις κορυφές  σε δύο παράλληλες ευθείες
σε δύο παράλληλες ευθείες και την κορυφή
 πάνω στην μεσοπαράλληλή τους . Αν η απόσταση των ευθειών είναι
πάνω στην μεσοπαράλληλή τους . Αν η απόσταση των ευθειών είναι  ,
,υπολογίστε το ελάχιστο μήκος της υποτείνουσας
 .
. έχει τις κορυφές
έχει τις κορυφές  σε δύο παράλληλες ευθείες
σε δύο παράλληλες ευθείες  πάνω στην μεσοπαράλληλή τους . Αν η απόσταση των ευθειών είναι
πάνω στην μεσοπαράλληλή τους . Αν η απόσταση των ευθειών είναι  ,
, .
.Χωρίς βλάβη οι συντεταγμένες των κορυφών είναι
 . H συνθήκη καθετότητας
. H συνθήκη καθετότητας  μεταφράζεται από τους συντελεστες διεύθυνσης σε
μεταφράζεται από τους συντελεστες διεύθυνσης σε  (άμεσο). Άρα
(άμεσο). Άρα  .
.  . Άρα γίνεται ελάχιστη όταν ελαχιστοποιηθεί το
. Άρα γίνεται ελάχιστη όταν ελαχιστοποιηθεί το  . To τελευταίο είναι απλό αφού
. To τελευταίο είναι απλό αφού  με ισότητα όταν
με ισότητα όταν  . Και λοιπά.
. Και λοιπά.Αλλιώς. Με τους συμβολισμούς του σχήματος τα τρίγωνα
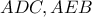 είναι όμοια, άρα
είναι όμοια, άρα 

 όταν
όταν 
 τα σημεία τομής της καθέτου από το
τα σημεία τομής της καθέτου από το  στις δύο παράλληλες .
στις δύο παράλληλες . είναι εγγράψιμο σε κύκλο
είναι εγγράψιμο σε κύκλο  . Η απόσταση
. Η απόσταση  από την «κάτω» παράλληλη είναι
από την «κάτω» παράλληλη είναι  .
. .
.
 ).
). .
. ,
,  (που ορίζουν διάμετρο του περιγεγραμμένου κύκλου) ευρίσκονται επί των παραλλήλων
(που ορίζουν διάμετρο του περιγεγραμμένου κύκλου) ευρίσκονται επί των παραλλήλων  ,
,  ,
, των
των  ,
,  .
. , και θα είναι
, και θα είναι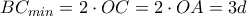
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες