 κινείται , έχοντας τα άκρα του
κινείται , έχοντας τα άκρα του  επί των ημιαξόνων
επί των ημιαξόνων  αντίστοιχα και έτσι ώστε :
αντίστοιχα και έτσι ώστε : . Ονομάζουμε
. Ονομάζουμε  το πρώτο σημείο στο οποίο η κάθετη της
το πρώτο σημείο στο οποίο η κάθετη της  στο
στο  , τέμνει τον
, τέμνει τον  .
.Να εκφράσετε το εμβαδόν του τριγώνου
 , ως συνάρτηση μιας μεταβλητής και να την μελετήσετε .
, ως συνάρτηση μιας μεταβλητής και να την μελετήσετε .

 η προβολή του
η προβολή του  Θέτω
Θέτω  οπότε
οπότε  και
και  Άρα,
Άρα, 
 απ' όπου παίρνω
απ' όπου παίρνω και το ζητούμενο εμβαδόν δίνεται από τη συνάρτηση
και το ζητούμενο εμβαδόν δίνεται από τη συνάρτηση με πεδίο ορισμού
με πεδίο ορισμού ![\boxed{{D_f} = \left[ {\frac{5}{{16}},\frac{{35}}{{16}}} \right]} \boxed{{D_f} = \left[ {\frac{5}{{16}},\frac{{35}}{{16}}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/7ff885dcf2f786953cc445280affa18a.png)
 Ολικό ελάχιστο
Ολικό ελάχιστο  στα σημεία
στα σημεία  και
και 
 στο σημείο
στο σημείο 
 στο
στο 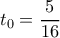 και
και  στο
στο 