 κινείται στην ανατολική "πλαγιά" του ημικυκλίου διαμέτρου
κινείται στην ανατολική "πλαγιά" του ημικυκλίου διαμέτρου 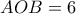 . Η εφαπτομένη
. Η εφαπτομένηστο
 , τέμνει την προέκταση της
, τέμνει την προέκταση της  στο σημείο
στο σημείο  και την μεσοκάθετη της χορδής
και την μεσοκάθετη της χορδής  στο
στο  .
.α) Πότε έχουμε :
 ; ... β) Ποια είναι η ελάχιστη τιμή του
; ... β) Ποια είναι η ελάχιστη τιμή του 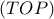 ;
; κινείται στην ανατολική "πλαγιά" του ημικυκλίου διαμέτρου
κινείται στην ανατολική "πλαγιά" του ημικυκλίου διαμέτρου 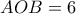 . Η εφαπτομένη
. Η εφαπτομένη , τέμνει την προέκταση της
, τέμνει την προέκταση της  στο σημείο
στο σημείο  και την μεσοκάθετη της χορδής
και την μεσοκάθετη της χορδής  στο
στο  .
. ; ... β) Ποια είναι η ελάχιστη τιμή του
; ... β) Ποια είναι η ελάχιστη τιμή του 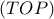 ;
; είναι πάντα κάθετη στην
είναι πάντα κάθετη στην  ως συμμετρική της ευθείας
ως συμμετρική της ευθείας  με άξονα την
με άξονα την  .
. και θα ισχύουν:
και θα ισχύουν:  Από το πιο πάνω σύστημα έχω δύο δεκτές λύσεις :
Από το πιο πάνω σύστημα έχω δύο δεκτές λύσεις : 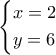 ή
ή  .
.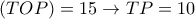 ,
,

 ( Από την υπόθεση). Θα είναι :
( Από την υπόθεση). Θα είναι : . Επίσης ,
. Επίσης ,  και έτσι έχει συντελεστή διεύθυνσης
και έτσι έχει συντελεστή διεύθυνσης  .
. έχει τετμημένη πάντα ,
έχει τετμημένη πάντα ,  το σημείο
το σημείο  προκύπτει από τη λύση του συστήματος :
προκύπτει από τη λύση του συστήματος : .
.  είναι :
είναι :  .
. 
 και είναι :
και είναι : 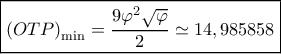
 ( εξ μάλλον και ο τίτλος) .
( εξ μάλλον και ο τίτλος) . , όπως στην ανάρτηση του α ερωτήματος
, όπως στην ανάρτηση του α ερωτήματος . Αλλά από το Θ. διχοτόμων στο
. Αλλά από το Θ. διχοτόμων στο  έχω:
έχω:
 κι έτσι προκύπτει η συνάρτηση του ζητουμένου εμβαδού :
κι έτσι προκύπτει η συνάρτηση του ζητουμένου εμβαδού : με παράγωγο:
με παράγωγο: 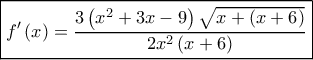
 παρουσιάζει ελάχιστο για
παρουσιάζει ελάχιστο για 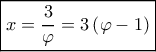 κ. λ. π.
κ. λ. π.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης