 Σε τμήμα
Σε τμήμα  , θεωρούμε σημείο
, θεωρούμε σημείο  , ώστε :
, ώστε :  . Γράφουμε τα ημικύκλια του σχήματος
. Γράφουμε τα ημικύκλια του σχήματοςκαι εν συνεχεία τον κόκκινο τρισεφαπτόμενο κύκλο
 . Δημιουργήστε συνάρτηση
. Δημιουργήστε συνάρτηση  ( του
( του  ) , η οποία
) , η οποία να αποδίδει την ακτίνα του κύκλου
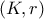 , βρείτε την μέγιστη τιμή της και το
, βρείτε την μέγιστη τιμή της και το  , για το οποίο :
, για το οποίο :  .
.
 είναι :
είναι :  .
.
 . Από το Θ
. Από το Θ  στο
στο  έχω:
έχω:  δηλαδή :
δηλαδή : και λύνω ως προς
και λύνω ως προς  παρουσιάζει μέγιστο για
παρουσιάζει μέγιστο για  το
το  ενώ αν
ενώ αν  θα έχω:
θα έχω:  καθ’ όσον το
καθ’ όσον το  βρίσκεται πιο κοντά στο
βρίσκεται πιο κοντά στο  ή στο
ή στο 
 (του κύκλου
(του κύκλου  ) μπορεί να γίνει και ως εξής:
) μπορεί να γίνει και ως εξής: . Πρόβλημα
. Πρόβλημα  του Απολλώνιου
του Απολλώνιου  και τα ημικύκλια
και τα ημικύκλια 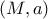 και
και  με μέσα
με μέσα  αντίστοιχα.
αντίστοιχα. τέμνονται στο
τέμνονται στο  και ο κύκλος
και ο κύκλος  τέμνει τα ημικύκλια
τέμνει τα ημικύκλια  στα
στα 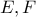 αντίστοιχα. Το
αντίστοιχα. Το  και η ακτίνα του
και η ακτίνα του 
