Καλημέρα σε όλους. Για το 1ο ερώτημα (δίχως συντεταγμένες), αλλά με αλγεβρικές μεθόδους. Χρονολογικά o Fermat έστειλε την επιστολή με τις μεθόδους για μέγιστα και ελάχιστα στον Descartes τον Δεκέμβριο του 1637, άρα τις μεθόδους αυτές τις θεωρώ προγενέστερες των Καρτεσιανών τεχνικών, άρα είμαι σύννομος (περίπτωση σπανιοτάτη) με τις προδιαγραφές του θεματοδότη. Στο 2ο ερώτημα καταφεύγω σε παραγώγους.


- 9-05-2021 Γεωμετρία.jpg (20.48 KiB) Προβλήθηκε 461 φορές
Για το 1ο:

Είναι

Είναι

, σταθερό, οπότε η παράσταση

παρουσιάζει ελάχιστο όταν

.
Τότε
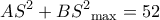
.
Γενική περίπτωση: 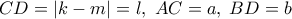

Είναι

Είναι

, σταθερό, οπότε η παράσταση

παρουσιάζει ελάχιστο όταν

.
Τότε

.
Για το 2ο:

Είναι

Η
![\displaystyle f:\left[ {0,6} \right] \to R,\;\;f\left( x \right) = {x^4} - 12{x^3} + 70{x^2} - 108x + 549 \displaystyle f:\left[ {0,6} \right] \to R,\;\;f\left( x \right) = {x^4} - 12{x^3} + 70{x^2} - 108x + 549](/forum/ext/geomar/texintegr/latexrender/pictures/07d04aa1e53d41df3079b2c3418306aa.png)
έχει παράγωγο

Με σχ. Horner εύκολα βρίσκουμε ρίζα

και με πίνακα προσήμου ότι η

έχει ελάχιστο το

, άρα

Γενική περίπτωση:
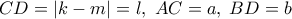

Η
![\displaystyle f:\left[ {0,l} \right] \to R,\;\;f\left( x \right) = {x^4} - 2l{x^3} + \left( {a + b + l} \right){x^2} - 2alx + a\left( {b + {l^2}} \right) \displaystyle f:\left[ {0,l} \right] \to R,\;\;f\left( x \right) = {x^4} - 2l{x^3} + \left( {a + b + l} \right){x^2} - 2alx + a\left( {b + {l^2}} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/30ed305dbcc98250daf4dba0cb89a0cb.png)
έχει παράγωγο

(και μετά έρχεται το λογισμικό...)
Αναρωτιέμαι, αν η παράσταση
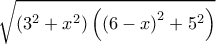
μπορεί να προσαρμοστεί ώστε να εφαρμόσουμε ανισότητα C-B-S.
 , βρίσκονται στο ίδιο ημιεπίπεδο ως προς μία ευθεία
, βρίσκονται στο ίδιο ημιεπίπεδο ως προς μία ευθεία  , επί της οποίας κινείται σημείο
, επί της οποίας κινείται σημείο  .
. για την οποία ελαχιστοποιείται το
για την οποία ελαχιστοποιείται το  , είναι θέμα πανέμορφο και πασίγνωστο .
, είναι θέμα πανέμορφο και πασίγνωστο . και
και 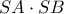 , προσπαθώντας να δώσουμε προκαρτεσιανή
, προσπαθώντας να δώσουμε προκαρτεσιανή και :
και :  .
.


 , σταθερό, οπότε η παράσταση
, σταθερό, οπότε η παράσταση  παρουσιάζει ελάχιστο όταν
παρουσιάζει ελάχιστο όταν  .
. 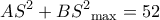 .
.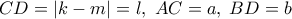


 , σταθερό, οπότε η παράσταση
, σταθερό, οπότε η παράσταση  παρουσιάζει ελάχιστο όταν
παρουσιάζει ελάχιστο όταν  .
.  .
.
![\displaystyle f:\left[ {0,6} \right] \to R,\;\;f\left( x \right) = {x^4} - 12{x^3} + 70{x^2} - 108x + 549 \displaystyle f:\left[ {0,6} \right] \to R,\;\;f\left( x \right) = {x^4} - 12{x^3} + 70{x^2} - 108x + 549](/forum/ext/geomar/texintegr/latexrender/pictures/07d04aa1e53d41df3079b2c3418306aa.png) έχει παράγωγο
έχει παράγωγο 
 και με πίνακα προσήμου ότι η
και με πίνακα προσήμου ότι η  έχει ελάχιστο το
έχει ελάχιστο το  , άρα
, άρα 

![\displaystyle f:\left[ {0,l} \right] \to R,\;\;f\left( x \right) = {x^4} - 2l{x^3} + \left( {a + b + l} \right){x^2} - 2alx + a\left( {b + {l^2}} \right) \displaystyle f:\left[ {0,l} \right] \to R,\;\;f\left( x \right) = {x^4} - 2l{x^3} + \left( {a + b + l} \right){x^2} - 2alx + a\left( {b + {l^2}} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/30ed305dbcc98250daf4dba0cb89a0cb.png)
 (και μετά έρχεται το λογισμικό...)
(και μετά έρχεται το λογισμικό...)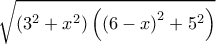 μπορεί να προσαρμοστεί ώστε να εφαρμόσουμε ανισότητα C-B-S.
μπορεί να προσαρμοστεί ώστε να εφαρμόσουμε ανισότητα C-B-S.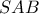 είναι
είναι  .
. σταθερό, θα έχουμε ελάχιστο όταν
σταθερό, θα έχουμε ελάχιστο όταν  , δηλαδή όταν
, δηλαδή όταν 
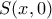 , οπότε
, οπότε 
 ,
, κ.ο.κ.
κ.ο.κ.