 είναι ορθογώνιο και ισοσκελές . Οι διάμεσοί του
είναι ορθογώνιο και ισοσκελές . Οι διάμεσοί του  ,
, τέμνονται στο
 . Υπολογίστε την :
. Υπολογίστε την :  . Αν οι διχοτόμοι των
. Αν οι διχοτόμοι των 
τέμνουν τις διαμέσους
 στα σημεία
στα σημεία  , υπολογίστε το
, υπολογίστε το  .
. είναι ορθογώνιο και ισοσκελές . Οι διάμεσοί του
είναι ορθογώνιο και ισοσκελές . Οι διάμεσοί του  ,
,  . Υπολογίστε την :
. Υπολογίστε την :  . Αν οι διχοτόμοι των
. Αν οι διχοτόμοι των 
 στα σημεία
στα σημεία  , υπολογίστε το
, υπολογίστε το  .
.
α) Η τρίτη διάμεσος
 είναι ύψος και διχοτόμος άρα με
είναι ύψος και διχοτόμος άρα με  ,
,  .
. .
. τέμνουν την υποτείνουσα
τέμνουν την υποτείνουσα  στα σημεία :
στα σημεία :  . Ας είναι δε
. Ας είναι δε  .
. με διατέμνουσα την
με διατέμνουσα την  και λαμβάνω υπ’ όψη ότι,
και λαμβάνω υπ’ όψη ότι, 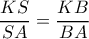 λόγω θ. διχοτόμου στο
λόγω θ. διχοτόμου στο  .Αν θέσω
.Αν θέσω  , έχω: :
, έχω: :  Από την
Από την  προκύπτει :
προκύπτει :  . Εκφράζω τώρα το
. Εκφράζω τώρα το  με δύο τρόπους :
με δύο τρόπους :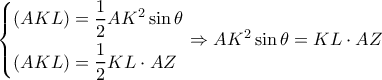 .
. η πιο πάνω γίνεται :
η πιο πάνω γίνεται : 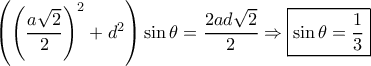 .
.Αλλιώς για το δεύτερο ερώτημα.
 με τις συντεταγμένες που φαίνονται στο σχήμα. Είναι
με τις συντεταγμένες που φαίνονται στο σχήμα. Είναι  άρα η
άρα η  έχει εξίσωση
έχει εξίσωση  ενώ η
ενώ η 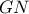 έχει εξίσωση
έχει εξίσωση  Λύνω το σύστημα
και βρίσκω
Λύνω το σύστημα
και βρίσκω 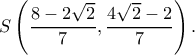 Εξάλλου,
Εξάλλου,  με
με 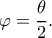 Παραλείποντας πράξεις,
Παραλείποντας πράξεις, απ' όπου
απ' όπου  και τελικά
και τελικά 
 του KARKAR , όποιος ..
του KARKAR , όποιος ..  τότε
τότε  και
και 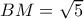 . Φέρω
. Φέρω  .
.  είναι εγγράψιμο οπότε
είναι εγγράψιμο οπότε 
 , ενώ
, ενώ  συνεπώς
συνεπώς 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες