KARKAR έγραψε: ↑Πέμ Απρ 15, 2021 6:52 pm
Μέγιστη προβολή.pngΗ κάθετη πλευρά

, του ορθογωνίου τριγώνου

είναι σταθερή , εν αντιθέσει με την

,
η οποία μεταβάλλεται . Φέροντας το ύψος

και την διχοτόμο

σχηματίζεται το τμήμα

,
του οποίου την προβολή

, στην

, ονομάζουμε

. Βρείτε την μέγιστη τιμή του τμήματος

.

- Μεγίστη προβολή_ok.png (17.21 KiB) Προβλήθηκε 404 φορές
Επιλέγω σύστημα συντεταγμένων με αρχή το

και μοναδιαίο του κατακόρυφου άξονα το διάνυσμα

.
Αν

προκύπτουν εύκολα :

και

, άρα:

κι έχει μέγιστο για

,

και είναι
Και είναι :

Αν το μήκος της σταθερής πλευράς

το πιο πάνω αποτέλεσμα προφανώς
πολλαπλασιάζεται με τη σταθερά αυτή.
Παρατήρηση :Ακριβώς,

 , του ορθογωνίου τριγώνου
, του ορθογωνίου τριγώνου  είναι σταθερή , εν αντιθέσει με την
είναι σταθερή , εν αντιθέσει με την  ,
, και την διχοτόμο
και την διχοτόμο  σχηματίζεται το τμήμα
σχηματίζεται το τμήμα  ,
, , στην
, στην  , ονομάζουμε
, ονομάζουμε  . Βρείτε την μέγιστη τιμή του τμήματος
. Βρείτε την μέγιστη τιμή του τμήματος  .
.
 και μοναδιαίο του κατακόρυφου άξονα το διάνυσμα
και μοναδιαίο του κατακόρυφου άξονα το διάνυσμα  .
. προκύπτουν εύκολα :
προκύπτουν εύκολα : και
και  , άρα:
, άρα: κι έχει μέγιστο για
κι έχει μέγιστο για  ,
,  και είναι
και είναι 
 το πιο πάνω αποτέλεσμα προφανώς
το πιο πάνω αποτέλεσμα προφανώς 
 και έστω
και έστω  η προβολή του
η προβολή του  στην
στην  Είναι
Είναι  και τα τρίγωνα
και τα τρίγωνα  είναι όμοια,
είναι όμοια,

 Αλλά,
Αλλά, 


 και
και 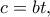 η
η  και με τη βοήθεια
και με τη βοήθεια  μέγιστο ίσο με
μέγιστο ίσο με 

 και
και 