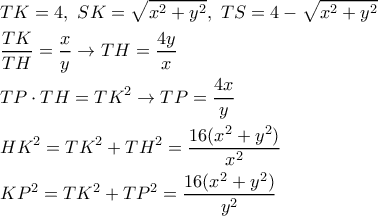KARKAR έγραψε: ↑Πέμ Απρ 08, 2021 7:53 pm
Ίχνη διχοτόμου.pngΣημείο

κινείται στο "δυτικό" ημικύκλιο , κύκλου

με εξίσωση :

. Η εφαπτομένη
του κύκλου στο

, τέμνει την ευθεία

, στο σημείο

. Η

είναι διχοτόμος στο τρίγωνο

.
Περιγράψτε επακριβώς - και με καρτεσιανή εξίσωση - τον γεωμετρικό τόπο του ίχνους

της διχοτόμου .
Θα ορίσω διαφορετικά το σημείο

και θα αποδείξω ότι είναι το ίδιο με το σημείο της εκφώνησης. Η
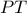
τέμνει την ευθεία
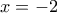
στο
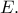
Από το

φέρνω παράλληλη στον

που τέμνει την ευθεία

στο

και την

στο
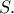
Προφανώς το

είναι το ορθόκεντρο του τριγώνου

Αλλά,

άρα

οπότε το

είναι σημείο της διχοτόμου της γωνίας

και εύκολα τώρα


- Ίχνη διχοτόμου.Ι.png (18.8 KiB) Προβλήθηκε 321 φορές
Άρα το

ισαπέχει από το σημείο

και από την ευθεία

που σημαίνει ότι κινείται σε μία παραβολή
με εστία το

και διευθετούσα την ευθεία

Η καρτεσιανή εξίσωση του τόπου είναι
 Διερεύνηση:
Διερεύνηση: Στο σχήμα ο γεωμετρικός τόπος είναι η κόκκινη καμπύλη. Τα σημεία

(

είναι η διάμετρος του
κύκλου πάνω στην ευθεία

) είναι οι οριακές θέσεις του τόπου, ενώ το σημείο

δεν είναι σημείο του
τόπου, καθόσον η εφαπτομένη του κύκλου στο

καθίσταται παράλληλη με τη ευθεία

 κινείται στο "δυτικό" ημικύκλιο , κύκλου
κινείται στο "δυτικό" ημικύκλιο , κύκλου  με εξίσωση :
με εξίσωση :  . Η εφαπτομένη
. Η εφαπτομένη , τέμνει την ευθεία
, τέμνει την ευθεία  , στο σημείο
, στο σημείο  . Η
. Η  είναι διχοτόμος στο τρίγωνο
είναι διχοτόμος στο τρίγωνο  .
. της διχοτόμου .
της διχοτόμου .
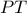 τέμνει την ευθεία
τέμνει την ευθεία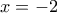 στο
στο 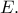 Από το
Από το  φέρνω παράλληλη στον
φέρνω παράλληλη στον  που τέμνει την ευθεία
που τέμνει την ευθεία  και την
και την  στο
στο 
 Αλλά,
Αλλά,  άρα
άρα 
 και εύκολα τώρα
και εύκολα τώρα 
 και από την ευθεία
και από την ευθεία  που σημαίνει ότι κινείται σε μία παραβολή
που σημαίνει ότι κινείται σε μία παραβολή  και διευθετούσα την ευθεία
και διευθετούσα την ευθεία  Η καρτεσιανή εξίσωση του τόπου είναι
Η καρτεσιανή εξίσωση του τόπου είναι 
 (
( είναι η διάμετρος του
είναι η διάμετρος του  δεν είναι σημείο του
δεν είναι σημείο του  καθίσταται παράλληλη με τη ευθεία
καθίσταται παράλληλη με τη ευθεία