Ρίζες πολυωνύμου

Γιώργος Μήτσιος · #1

Χαιρετώ.

Ας θεωρήσουμε το πολυώνυμο $P(x)=x^{3} +x^{2}-\Phi^{5} x +\Phi ^{5 }$ , όπου $\Phi=2\sigma \upsilon \nu \dfrac{\pi }{5}$ ( ο χρυσός αριθμός ).

Να βρεθούν οι ρίζες του . Ζητείται και λύση χωρίς χρήση παραγώγου.

Σας ευχαριστώ, Γιώργος.

Manolis Petrakis · #2

Μία προφανής(;) ρίζα είναι το $\phi$ διότι αν $x=\phi$ τότε $P(x)=(\phi^3+\phi^2)-\phi^6+\phi^5=\phi^4-\phi^6+\phi^5=\phi^4(\phi^2-\phi-1)=0$
Τωρα με σχήμα Horner

:
$P(x)=[x^2+(1+\phi)x+\phi^2+\phi-\phi^5](x-\phi)$
Έτσι αρκεί να λύσουμε τη δευτεροβάθμια $x^2+(1+\phi)x+\phi^2+\phi-\phi^5=0\Leftrightarrow x^2+\phi^2x+\phi^3-\phi^5=0\Leftrightarrow x^2+\phi^2x+\phi^3(\phi^2-1)=0$
$\Leftrightarrow x^2+\phi^2x-\phi^4=0$ με $\Delta=5\phi^4$
Έτσι $x=\dfrac{-\phi^2-\phi^2\sqrt 5}{2}=-\phi^2\dfrac{1+\sqrt 5}{2}=-\phi^3$
Ή $x=\dfrac{-\phi^2+\phi^2\sqrt 5}{2}=\phi^2\dfrac{\sqrt 5-1}{2}=\phi$
* Είναι γνωστό ότι $\phi =\dfrac{\sqrt 5+1}{2},\dfrac{1}{\phi}=\dfrac{\sqrt 5-1}{2}$
Αλλά και ότι $\phi^{n+2}=\phi^{n+1}+\phi^n$ με $n\in \mathbb{N}$

#3

Γιώργος Μήτσιος έγραψε: ↑
Σάβ Φεβ 13, 2021 6:09 pm
Χαιρετώ.

Ας θεωρήσουμε το πολυώνυμο $P(x)=x^{3} +x^{2}-\Phi^{5} x +\Phi ^{5 }$ , όπου $\Phi=2\sigma \upsilon \nu \dfrac{\pi }{5}$ ( ο χρυσός αριθμός ).

Να βρεθούν οι ρίζες του . Ζητείται και λύση χωρίς χρήση παραγώγου.

Σας ευχαριστώ, Γιώργος.

$\displaystyle \left\{ \begin{array}{l} {\Phi ^2} = \Phi + 1\\ {\Phi ^3} = {\Phi ^2} + \Phi = 2\Phi + 1 \end{array} \right. \Rightarrow {\Phi ^5} = 2{\Phi ^2} + 3\Phi + 1 \Leftrightarrow$ $\boxed{{\Phi ^5} = 5\Phi + 3}$

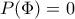Εύκολα τώρα διαπιστώνω ότι $\displaystyle P(\Phi ) = 0$ και με Horner καταλήγω στην εξίσωση:

$\displaystyle {x^2} + {\Phi ^2}x - (2{\Phi ^2} + \Phi ) = 0 \Leftrightarrow x = \frac{{ - {\Phi ^2} \pm \sqrt {9{\Phi ^2} + 6\Phi + 1} }}{2} \Leftrightarrow x = \frac{{ - (\Phi + 1) \pm (3\Phi + 1)}}{2}$

Άρα, τελικά έχουμε $\boxed{x = \Phi = \frac{{\sqrt 5 + 1}}{2}}$ διπλή ρίζα και $\boxed{x = - 1 - 2\Phi = - 2 - \sqrt 5}$

Με πρόλαβε ο Μανώλης. Το αφήνω για τον κόπο.

Ρίζες πολυωνύμου

Ρίζες πολυωνύμου

Re: Ρίζες πολυωνύμου

Re: Ρίζες πολυωνύμου

Μέλη σε σύνδεση