 , το οποίο κινείται στον ημιάξονα
, το οποίο κινείται στον ημιάξονα  , εφάπτεται του τμήματος
, εφάπτεται του τμήματος  .
.Φέρουμε τα εφαπτόμενα τμήματα
 . Υπολογίστε το μέγιστο του τμήματος
. Υπολογίστε το μέγιστο του τμήματος  .
.Δώστε αριθμητικό παράδειγμα .
 , το οποίο κινείται στον ημιάξονα
, το οποίο κινείται στον ημιάξονα  , εφάπτεται του τμήματος
, εφάπτεται του τμήματος  .
. . Υπολογίστε το μέγιστο του τμήματος
. Υπολογίστε το μέγιστο του τμήματος  .
.Ας είναι
 . Η ευθεία
. Η ευθεία  έχει εξίσωση :
έχει εξίσωση : 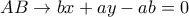 .
. .
.  και η πολική,
και η πολική,  της αρχής ως προς αυτόν έχει εξίσωση :
της αρχής ως προς αυτόν έχει εξίσωση : και άρα
και άρα 
 θα έχω και λόγω της
θα έχω και λόγω της  :
:
 για να έχω μέγιστο και το μέγιστο μετά.
για να έχω μέγιστο και το μέγιστο μετά. προκύπτει :
προκύπτει : ![\boxed{k = \sqrt[3]{{\frac{{15\sqrt {129} }}{8} + \frac{{1341}}{{64}}}} - \sqrt[3]{{\frac{{15\sqrt {129} }}{8} - \frac{{1341}}{{64}}}} - \frac{3}{4}} \boxed{k = \sqrt[3]{{\frac{{15\sqrt {129} }}{8} + \frac{{1341}}{{64}}}} - \sqrt[3]{{\frac{{15\sqrt {129} }}{8} - \frac{{1341}}{{64}}}} - \frac{3}{4}}](/forum/ext/geomar/texintegr/latexrender/pictures/712be90b807a7a0c22e64c1bc194655a.png)
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες