 , τετραγώνου
, τετραγώνου  κατά τμήμα
κατά τμήμα  . Σημείο
. Σημείο 
κινείται επί της
 και έστω
και έστω  η προβολή του στην
η προβολή του στην  . Υπολογίστε το :
. Υπολογίστε το :  .
.Υπάρχει τιμή του
 για την οποία το εμβαδόν μεγιστοποιείται , όταν το
για την οποία το εμβαδόν μεγιστοποιείται , όταν το  συμπέσει με το
συμπέσει με το  ;
; , τετραγώνου
, τετραγώνου  κατά τμήμα
κατά τμήμα  . Σημείο
. Σημείο 
 και έστω
και έστω  η προβολή του στην
η προβολή του στην  . Υπολογίστε το :
. Υπολογίστε το :  .
. για την οποία το εμβαδόν μεγιστοποιείται , όταν το
για την οποία το εμβαδόν μεγιστοποιείται , όταν το  συμπέσει με το
συμπέσει με το  ;
; .
. . Έστω
. Έστω  , οπότε
, οπότε  .
.![\displaystyle f\left( t \right) = - {t^2} + \left( {2k - 1} \right)at + 2{a^2}k,\;\;t \in \left[ {0,\;ka} \right] \displaystyle f\left( t \right) = - {t^2} + \left( {2k - 1} \right)at + 2{a^2}k,\;\;t \in \left[ {0,\;ka} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/475c5c33f59debf14256abf9880d58ea.png) έχει παράγωγο
έχει παράγωγο  , οπότε μεγιστοποιείται για
, οπότε μεγιστοποιείται για  , άρα
, άρα 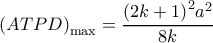 .
. έχει εμβαδόν
έχει εμβαδόν  , οπότε όταν αυξάνει το
, οπότε όταν αυξάνει το  , αυξάνει και το εμβαδόν.
, αυξάνει και το εμβαδόν. , το εμβαδόν του γίνεται
, το εμβαδόν του γίνεται  .
. είναι
είναι  ,
, 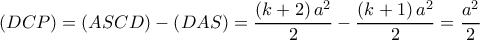 , σταθερό, οπότε δεν υπάρχει τιμή του
, σταθερό, οπότε δεν υπάρχει τιμή του  για την οποία να μεγιστοποιείται το
για την οποία να μεγιστοποιείται το  ως προς το
ως προς το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες