 έχει σταθερή την πλευρά
έχει σταθερή την πλευρά  και μεταβλητή την
και μεταβλητή την  .
.Οι διχοτόμοι των γωνιών
 αλληλοτεμνόμενες , σχηματίζουν
αλληλοτεμνόμενες , σχηματίζουν το παραλληλόγραμμο
 , του οποίου ψάχνουμε το μέγιστο εμβαδόν .
, του οποίου ψάχνουμε το μέγιστο εμβαδόν . έχει σταθερή την πλευρά
έχει σταθερή την πλευρά  και μεταβλητή την
και μεταβλητή την  .
. αλληλοτεμνόμενες , σχηματίζουν
αλληλοτεμνόμενες , σχηματίζουν  , του οποίου ψάχνουμε το μέγιστο εμβαδόν .
, του οποίου ψάχνουμε το μέγιστο εμβαδόν . . Ακριβέστερα, αν
. Ακριβέστερα, αν 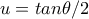 , τότε έχουμε μεγιστοποίηση εμβαδού παραλληλογράμμου για εκείνο το
, τότε έχουμε μεγιστοποίηση εμβαδού παραλληλογράμμου για εκείνο το  (και
(και  ) για το οποίο ισχύει η
) για το οποίο ισχύει η  . Αυτό προκύπτει από την ισότητα του ζητούμενου εμβαδού προς
. Αυτό προκύπτει από την ισότητα του ζητούμενου εμβαδού προς  . Το μέγιστο εμβαδόν ισούται προς περίπου
. Το μέγιστο εμβαδόν ισούται προς περίπου  .
.Με ενημερώνει ο προτείνων KARKAR ότι το δικό του αποτέλεσμα διαφέρει ελαφρά από το δικό μου: θα ξαναδώ τους υπολογισμούς μου και θα επανέλθω!gbaloglou έγραψε: ↑Κυρ Νοέμ 10, 2019 10:58 pmΒρίσκω ότι η μέγιστη τιμή αντιστοιχεί σε γωνία. Ακριβέστερα, αν
, τότε έχουμε μεγιστοποίηση εμβαδού παραλληλογράμμου για εκείνο το
(και
) για το οποίο ισχύει η
. Αυτό προκύπτει από την ισότητα του ζητούμενου εμβαδού προς
. Το μέγιστο εμβαδόν ισούται προς περίπου
.
[Χρησιμοποίησα αναλυτική γεωμετρία και εξωτερικό γινόμενο διανυσμάτων. Επειδή οι πράξεις είναι πολλές, δεν δίνω λεπτομέρειες ... μέχρις ότου επιβεβαιώσει κάποιος το παραπάνω αποτέλεσμα μέσω geogebra ή άλλου πακέτου.]
Πράγματι βρήκα ένα μικρό λάθος στους υπολογισμούς μου, εξακολουθώ όμως -- παρά τις προσπάθειες και τους ελέγχους -- να έχω μια μικρή διαφορά από το αποτέλεσμα του Θανάση (gbaloglou έγραψε: ↑Δευ Νοέμ 11, 2019 8:14 amΜε ενημερώνει ο προτείνων KARKAR ότι το δικό του αποτέλεσμα διαφέρει ελαφρά από το δικό μου: θα ξαναδώ τους υπολογισμούς μου και θα επανέλθω!gbaloglou έγραψε: ↑Κυρ Νοέμ 10, 2019 10:58 pmΒρίσκω ότι η μέγιστη τιμή αντιστοιχεί σε γωνία. Ακριβέστερα, αν
, τότε έχουμε μεγιστοποίηση εμβαδού παραλληλογράμμου για εκείνο το
(και
) για το οποίο ισχύει η
. Αυτό προκύπτει από την ισότητα του ζητούμενου εμβαδού προς
. Το μέγιστο εμβαδόν ισούται προς περίπου
.
[Χρησιμοποίησα αναλυτική γεωμετρία και εξωτερικό γινόμενο διανυσμάτων. Επειδή οι πράξεις είναι πολλές, δεν δίνω λεπτομέρειες ... μέχρις ότου επιβεβαιώσει κάποιος το παραπάνω αποτέλεσμα μέσω geogebra ή άλλου πακέτου.]
 ), και υπάρχουν λόγοι να πιστεύουμε ότι το λάθος βρίσκεται στο δικό μου αποτέλεσμα (
), και υπάρχουν λόγοι να πιστεύουμε ότι το λάθος βρίσκεται στο δικό μου αποτέλεσμα ( ). Για την ιστορία, το εμβαδόν που έχω τώρα είναι το
). Για την ιστορία, το εμβαδόν που έχω τώρα είναι το  : δεν ξέρω αν και πότε θα το ξαναπροσπαθήσω...
: δεν ξέρω αν και πότε θα το ξαναπροσπαθήσω...Με Geogebra, επιβεβαιώνεται η γωνία σου Γιώργο,gbaloglou έγραψε: ↑Δευ Νοέμ 11, 2019 1:03 pmΠράγματι βρήκα ένα μικρό λάθος στους υπολογισμούς μου, εξακολουθώ όμως -- παρά τις προσπάθειες και τους ελέγχους -- να έχω μια μικρή διαφορά από το αποτέλεσμα του Θανάση (gbaloglou έγραψε: ↑Δευ Νοέμ 11, 2019 8:14 amΜε ενημερώνει ο προτείνων KARKAR ότι το δικό του αποτέλεσμα διαφέρει ελαφρά από το δικό μου: θα ξαναδώ τους υπολογισμούς μου και θα επανέλθω!gbaloglou έγραψε: ↑Κυρ Νοέμ 10, 2019 10:58 pmΒρίσκω ότι η μέγιστη τιμή αντιστοιχεί σε γωνία. Ακριβέστερα, αν
, τότε έχουμε μεγιστοποίηση εμβαδού παραλληλογράμμου για εκείνο το
(και
) για το οποίο ισχύει η
. Αυτό προκύπτει από την ισότητα του ζητούμενου εμβαδού προς
. Το μέγιστο εμβαδόν ισούται προς περίπου
.
[Χρησιμοποίησα αναλυτική γεωμετρία και εξωτερικό γινόμενο διανυσμάτων. Επειδή οι πράξεις είναι πολλές, δεν δίνω λεπτομέρειες ... μέχρις ότου επιβεβαιώσει κάποιος το παραπάνω αποτέλεσμα μέσω geogebra ή άλλου πακέτου.]), και υπάρχουν λόγοι να πιστεύουμε ότι το λάθος βρίσκεται στο δικό μου αποτέλεσμα (
). Για την ιστορία, το εμβαδόν που έχω τώρα είναι το
: δεν ξέρω αν και πότε θα το ξαναπροσπαθήσω...

!!! The plot thickens, όπως λέγαμε και εν ΗΠΑgeorge visvikis έγραψε: ↑Δευ Νοέμ 11, 2019 1:51 pmΜε Geogebra, επιβεβαιώνεται η γωνία σου Γιώργο,gbaloglou έγραψε: ↑Δευ Νοέμ 11, 2019 1:03 pmΠράγματι βρήκα ένα μικρό λάθος στους υπολογισμούς μου, εξακολουθώ όμως -- παρά τις προσπάθειες και τους ελέγχους -- να έχω μια μικρή διαφορά από το αποτέλεσμα του Θανάση (gbaloglou έγραψε: ↑Δευ Νοέμ 11, 2019 8:14 amΜε ενημερώνει ο προτείνων KARKAR ότι το δικό του αποτέλεσμα διαφέρει ελαφρά από το δικό μου: θα ξαναδώ τους υπολογισμούς μου και θα επανέλθω!gbaloglou έγραψε: ↑Κυρ Νοέμ 10, 2019 10:58 pmΒρίσκω ότι η μέγιστη τιμή αντιστοιχεί σε γωνία. Ακριβέστερα, αν
, τότε έχουμε μεγιστοποίηση εμβαδού παραλληλογράμμου για εκείνο το
(και
) για το οποίο ισχύει η
. Αυτό προκύπτει από την ισότητα του ζητούμενου εμβαδού προς
. Το μέγιστο εμβαδόν ισούται προς περίπου
.
[Χρησιμοποίησα αναλυτική γεωμετρία και εξωτερικό γινόμενο διανυσμάτων. Επειδή οι πράξεις είναι πολλές, δεν δίνω λεπτομέρειες ... μέχρις ότου επιβεβαιώσει κάποιος το παραπάνω αποτέλεσμα μέσω geogebra ή άλλου πακέτου.]), και υπάρχουν λόγοι να πιστεύουμε ότι το λάθος βρίσκεται στο δικό μου αποτέλεσμα (
). Για την ιστορία, το εμβαδόν που έχω τώρα είναι το
: δεν ξέρω αν και πότε θα το ξαναπροσπαθήσω...

Ένας τρόπος υπολογισμού του εμβαδού του παραλληλογράμμου
 είναι η χρήση εξωτερικού γινομένου διανυσμάτων, οπότε
είναι η χρήση εξωτερικού γινομένου διανυσμάτων, οπότε  , όπου
, όπου  ,
,  . (Βλέπε πχ εδώ.)
. (Βλέπε πχ εδώ.) ,
,  ,
,  ),
),  . Θέτοντας επίσης
. Θέτοντας επίσης  , βρίσκουμε εύκολα τις εξισώσεις των τεσσάρων πλευρών του
, βρίσκουμε εύκολα τις εξισώσεις των τεσσάρων πλευρών του  :
:  ,
, 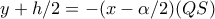 ,
,  ,
,  .
.



 ,
,  :
:
 στην
στην  καταλήγουμε στον τύπο εμβαδού
καταλήγουμε στον τύπο εμβαδού  που έδωσα νωρίτερα σήμερα. Θέτοντας
που έδωσα νωρίτερα σήμερα. Θέτοντας  , οπότε
, οπότε  , παρατηρούμε ότι η
, παρατηρούμε ότι η  είναι ισοδύναμη προς την
είναι ισοδύναμη προς την  , εξίσωση που οδηγεί στην
, εξίσωση που οδηγεί στην  (μόνη πραγματική ρίζα) και στην
(μόνη πραγματική ρίζα) και στην  .
. , και αντιστοιχεί σε ορθογώνιο ύψους
, και αντιστοιχεί σε ορθογώνιο ύψους  .
. , έχω :
, έχω :  . Βρίσκουμε την εξίσωση της
. Βρίσκουμε την εξίσωση της  : Σημείο
: Σημείο 
 , που δίνει την ( δεκτή ) λύση :
, που δίνει την ( δεκτή ) λύση : 
 ως τομή των
ως τομή των  , έχει συντεταγμένες :
, έχει συντεταγμένες : 
 και εν συνεχεία το εμβαδόν του τριγώνου
και εν συνεχεία το εμβαδόν του τριγώνου 
 δεν μου χρειάζεται ! - με τον τύπο της ορίζουσας , το διπλάσιο του οποίου είναι το ζητούμενο .
δεν μου χρειάζεται ! - με τον τύπο της ορίζουσας , το διπλάσιο του οποίου είναι το ζητούμενο . και η μεγιστοποίησή του βρίσκεται με χρήση λογισμικού ...
και η μεγιστοποίησή του βρίσκεται με χρήση λογισμικού ...Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες