 , θεωρούμε σημεία
, θεωρούμε σημεία 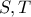 , τέτοια ώστε :
, τέτοια ώστε :  και
και ονομάζουμε
 τις προβολές τους στην
τις προβολές τους στην  . Η
. Η  τέμνει την
τέμνει την  στο σημείο
στο σημείο  .
.Ενδιαφερόμαστε για την μεγιστοποίηση του εμβαδού του τραπεζίου
 ...
... , θεωρούμε σημεία
, θεωρούμε σημεία 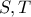 , τέτοια ώστε :
, τέτοια ώστε :  και
και  τις προβολές τους στην
τις προβολές τους στην  . Η
. Η  τέμνει την
τέμνει την  στο σημείο
στο σημείο  .
. ...
...Έστω
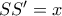 και
και  η ακτίνα του τεταρτοκυκλίου. Προφανώς,
η ακτίνα του τεταρτοκυκλίου. Προφανώς, 
 και
και 
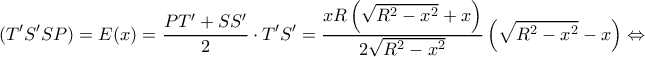
 με παράγωγο
με παράγωγο 
 μέγιστη τιμή ίση με
μέγιστη τιμή ίση με 


 (ορθογώνια τρίγωνα ΟΤΤ΄ και OPT΄).
(ορθογώνια τρίγωνα ΟΤΤ΄ και OPT΄). =
= 
 , που μηδενίζεται για
, που μηδενίζεται για  , με δεκτή τιμή (θ στο πρώτο τεταρτημόριο)
, με δεκτή τιμή (θ στο πρώτο τεταρτημόριο)  . (θ = περίπου 25.91 μοίρες).
. (θ = περίπου 25.91 μοίρες). είναι αρνητική για κάθε θ (στο πρώτο τεταρτημόριο).
είναι αρνητική για κάθε θ (στο πρώτο τεταρτημόριο). το Ε(θ) έχει μέγιστο, που είναι
το Ε(θ) έχει μέγιστο, που είναι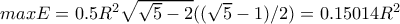 . Τούτο είναι ίδιο με της # 2 (george visvikis).
. Τούτο είναι ίδιο με της # 2 (george visvikis).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες