 υπάρχουν ώστε
υπάρχουν ώστε  και
και 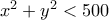 ;
;Aς την αφήσουμε
 ώρες για τους μαθητές μας. Θα έλεγα ότι είναι προσιτή και για μαθητές Γυμνασίου.
ώρες για τους μαθητές μας. Θα έλεγα ότι είναι προσιτή και για μαθητές Γυμνασίου. ζεύγη
ζεύγη  , υποθέτοντας ωστόσο πως ο
, υποθέτοντας ωστόσο πως ο  είναι τέλειο τετράγωνο. Αυτό το εξήγαγα απο την σχέση
είναι τέλειο τετράγωνο. Αυτό το εξήγαγα απο την σχέση  (όπου
(όπου  ακέραιος ώστε
ακέραιος ώστε  ) στην οποία εύκολα καταλήγουμε με λίγες πράξεις. Η υπόθεσή μου είναι σωστή;
) στην οποία εύκολα καταλήγουμε με λίγες πράξεις. Η υπόθεσή μου είναι σωστή;Καλή η προσπάθεια αλλά έχει δρόμο ακόμα. Πρώτα απ' όλα στις διατυπώσεις διότι κάνεις τα εύκολα, δύσκολα. Π.χ. αντί να λες "ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Πέμ Δεκ 13, 2018 12:10 amΈχω βρεί μία λύση με αποτέλεσμαζεύγη
, υποθέτοντας ωστόσο πως ο
είναι τέλειο τετράγωνο. Αυτό το εξήγαγα απο την σχέση
(όπου
ακέραιος ώστε
) στην οποία εύκολα καταλήγουμε με λίγες πρέξεις. Η υπόθεσή μου είναι σωστή;
 είναι τέλειο τετράγωνο" και μετά να γράφεις
είναι τέλειο τετράγωνο" και μετά να γράφεις  στις παραστάσεις, βάλε
στις παραστάσεις, βάλε 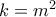 για να τελειώνουμε. Τώρα αντί για
για να τελειώνουμε. Τώρα αντί για  απλά θα έχεις
απλά θα έχεις  .
.  ζεύγη. Είναι άμεσο ότι υπάρχουν και άλλα, π.χ
ζεύγη. Είναι άμεσο ότι υπάρχουν και άλλα, π.χ  ή
ή 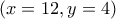 ή
ή  και άλλα.
και άλλα.Σας ευχαριστώ κύριε Μιχάλη για τις παρατηρήσεις. Όσο για την άσκηση... θα την ξανακοιτάξωMihalis_Lambrou έγραψε: ↑Πέμ Δεκ 13, 2018 1:15 amΚαλή η προσπάθεια αλλά έχει δρόμο ακόμα. Πρώτα απ' όλα στις διατυπώσεις διότι κάνεις τα εύκολα, δύσκολα. Π.χ. αντί να λες "ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Πέμ Δεκ 13, 2018 12:10 amΈχω βρεί μία λύση με αποτέλεσμαζεύγη
, υποθέτοντας ωστόσο πως ο
είναι τέλειο τετράγωνο. Αυτό το εξήγαγα απο την σχέση
(όπου
ακέραιος ώστε
) στην οποία εύκολα καταλήγουμε με λίγες πρέξεις. Η υπόθεσή μου είναι σωστή;
είναι τέλειο τετράγωνο" και μετά να γράφεις
στις παραστάσεις, βάλε
για να τελειώνουμε. Τώρα αντί για
απλά θα έχεις
.
Επίσης, το αποτέλεσμα δεν είναι μόνοζεύγη. Είναι άμεσο ότι υπάρχουν και άλλα, π.χ
ή
ή
και άλλα.

 , όπου
, όπου  και
και  , όπου
, όπου  . Aντικαθιστώντας έχουμε
. Aντικαθιστώντας έχουμε 
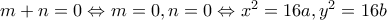 .Άρα
.Άρα 
 πράγμα άτοπο). Πρέπει να βρούμε το πλήθος των πιθανών ζεύγων
πράγμα άτοπο). Πρέπει να βρούμε το πλήθος των πιθανών ζεύγων  ώστε
ώστε  με
με  και
και  αφού
αφού  .
. άρα ο
άρα ο  ορίζεται με
ορίζεται με 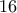 τρόπους.Η μέγιστη τιμή του
τρόπους.Η μέγιστη τιμή του  είναι η
είναι η  ενώ η ελάχιστη
ενώ η ελάχιστη  . Άρα ο
. Άρα ο  ορίζεται με
ορίζεται με 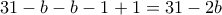 τρόπους κι επειδή αυτό ορίζεται με
τρόπους κι επειδή αυτό ορίζεται με 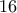 τρόπους για τους
τρόπους για τους 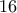 τρόπους που ορίζεται ο
τρόπους που ορίζεται ο  .Άρα έχουμε
.Άρα έχουμε  ζεύγη
ζεύγη 
 . Eδώ με το ίδιο σκεπτικό με πριν βρίσκουμε
. Eδώ με το ίδιο σκεπτικό με πριν βρίσκουμε  ζεύγη.
ζεύγη. ζεύγη
ζεύγη Χμμμμ.ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Σάβ Δεκ 15, 2018 12:36 amΈχουμε:
Έστω πως, όπου
και
, όπου
. Aντικαθιστώντας έχουμε

.Άρα

(πράγμα άτοπο). Πρέπει να βρούμε το πλήθος των πιθανών ζεύγων
ώστε
με
και
αφού
.
Παρατηρούμε ότι πρέπειάρα ο
ορίζεται με
τρόπους.Η μέγιστη τιμή του
είναι η
ενώ η ελάχιστη
. Άρα ο
ορίζεται με
τρόπους κι επειδή αυτό ορίζεται με
τρόπους για τους
τρόπους που ορίζεται ο
.Άρα έχουμε
ζεύγη
Άρα συνολικά έχουμε
. Eδώ με το ίδιο σκεπτικό με πριν βρίσκουμε
ζεύγη.
ζεύγη
,που είναι το λάθος;
 από όπου επικεντρώθηκες στην εκδοχή
από όπου επικεντρώθηκες στην εκδοχή  . Από εκεί συμπεραίνεις
. Από εκεί συμπεραίνεις  .
. , από όπου
, από όπου  . Σωστά;
. Σωστά;  , αλλά το
, αλλά το 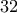 δεν είναι τέλειο τετράγωνο. Οπότε κακώς το μέτρησες ως λύση.
δεν είναι τέλειο τετράγωνο. Οπότε κακώς το μέτρησες ως λύση.  είναι τέλεια τετράγωνα, και εργάστηκες σαν να ήσαν απλοί αριθμοί, χωρίς περιορισμό.
είναι τέλεια τετράγωνα, και εργάστηκες σαν να ήσαν απλοί αριθμοί, χωρίς περιορισμό. άρα και ο
άρα και ο  και ο
και ο  είναι τέλεια τετράγωνα. Είναι
είναι τέλεια τετράγωνα. Είναι  και
και  .
.
 έχουμε
έχουμε  τιμές για το
τιμές για το 
 έχουμε
έχουμε  τιμές για το
τιμές για το 
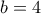 έχουμε
έχουμε  τιμές για το
τιμές για το 
 έχουμε
έχουμε  τιμή για το
τιμή για το 
 έχουμε
έχουμε  ζεύγη
ζεύγη  .
. και
και  φαίνεται αρκετά επίπονο και χρονοβόρο
φαίνεται αρκετά επίπονο και χρονοβόρο  είναι είτε και οι δύο άρτιοι είτα και οι δύο περιττοί.
είναι είτε και οι δύο άρτιοι είτα και οι δύο περιττοί. είναι και οι δύο περιττοί.
είναι και οι δύο περιττοί. . Κάνε τώρα ακριβώς ίδιες σκέψεις με τους
. Κάνε τώρα ακριβώς ίδιες σκέψεις με τους  στην θέση των
στην θέση των  .
.Για να κλείνει: Αφού
 άρτιος, οι
άρτιος, οι  πρέπει να είναι είτε και οι δύο άρτιοι είτε και οι δύο περιττοί. Η δεύτερη περίπτωση αποκλείεται διότι
πρέπει να είναι είτε και οι δύο άρτιοι είτε και οι δύο περιττοί. Η δεύτερη περίπτωση αποκλείεται διότι  , που δεν γίνεται. Άρα
, που δεν γίνεται. Άρα  . Έτσι
. Έτσι  , οπότε
, οπότε  . Με ακριβώς τον ίδιο τρόπο καταλήγουμε
. Με ακριβώς τον ίδιο τρόπο καταλήγουμε  οπότε
οπότε 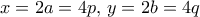 . Άρα
. Άρα  , ή αλλιώς
, ή αλλιώς  . Ειδικά
. Ειδικά  , και έτσι οι αποδεκτές τιμές προκύπτουν με άμεσο (αλλά ανιαρό) έλεγχο μικρών περιπτώσεων. Τέτοιες είναι οι
, και έτσι οι αποδεκτές τιμές προκύπτουν με άμεσο (αλλά ανιαρό) έλεγχο μικρών περιπτώσεων. Τέτοιες είναι οι  ίσον
ίσον  . Από αυτές επιλέγουμε τις
. Από αυτές επιλέγουμε τις  που ικανοποιούν την συνθήκη
που ικανοποιούν την συνθήκη  της υπόθεσης. Μετράμε.
της υπόθεσης. Μετράμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες