 είναι ένα σημείο της πλευράς
είναι ένα σημείο της πλευράς  τριγώνου
τριγώνου  ώστε
ώστε  Τα σημεία
Τα σημεία 
και τα βαρύκεντρα
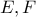 των τριγώνων
των τριγώνων  είναι ομοκυκλικά. Να δείξετε ότι
είναι ομοκυκλικά. Να δείξετε ότι 
Σημείωση: Το σχήμα δεν είναι ακριβές.
 είναι ένα σημείο της πλευράς
είναι ένα σημείο της πλευράς  τριγώνου
τριγώνου  ώστε
ώστε  Τα σημεία
Τα σημεία 
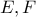 των τριγώνων
των τριγώνων  είναι ομοκυκλικά. Να δείξετε ότι
είναι ομοκυκλικά. Να δείξετε ότι 
Καλησπέρα Γιώργο.george visvikis έγραψε: ↑Τετ Αύγ 15, 2018 7:06 pmείναι ένα σημείο της πλευράς
τριγώνου
ώστε
Τα σημεία

και τα βαρύκεντρατων τριγώνων
είναι ομοκυκλικά. Να δείξετε ότι
Σημείωση: Το σχήμα δεν είναι ακριβές.
 τέμνουν (ως διάμεσοι) την
τέμνουν (ως διάμεσοι) την  στο μέσο της. Έστω λοιπόν
στο μέσο της. Έστω λοιπόν  .
. . Όμως, ισχύει
. Όμως, ισχύει  . Αντικαθιστώντας, προκύπτει
. Αντικαθιστώντας, προκύπτει  .
. , ή ισοδύναμα
, ή ισοδύναμα  , όμως, από την Τριγωνική Ανισότητα,
, όμως, από την Τριγωνική Ανισότητα, , άρα αναγκαστικά
, άρα αναγκαστικά 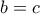 , το ζητούμενο.
, το ζητούμενο.Ορέστης Λιγνός έγραψε: ↑Τετ Αύγ 15, 2018 11:10 pmΚαλησπέρα Γιώργο.george visvikis έγραψε: ↑Τετ Αύγ 15, 2018 7:06 pmΚριτήριο ισοσκελούς.2.png
είναι ένα σημείο της πλευράς
τριγώνου
ώστε
Τα σημεία

και τα βαρύκεντρατων τριγώνων
είναι ομοκυκλικά. Να δείξετε ότι
Σημείωση: Το σχήμα δεν είναι ακριβές.
Προφανώς, οιτέμνουν (ως διάμεσοι) την
στο μέσο της. Έστω λοιπόν
.
Τότε, από δύναμη σημείου. Όμως, ισχύει
. Αντικαθιστώντας, προκύπτει
.
Από Θ. Διαμέσων,, ή ισοδύναμα
, όμως, από την Τριγωνική Ανισότητα,
, άρα αναγκαστικά
, το ζητούμενο.
 το μέσο της
το μέσο της  , όπου δηλ. τέμνονται και οι
, όπου δηλ. τέμνονται και οι  και
και 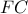 . Εστω επίσης
. Εστω επίσης  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα. και
και  . Αρα
. Αρα  . Αρα
. Αρα  ισοσκελές τραπέζιο (επειδή εγγράφεται) και επομένως
ισοσκελές τραπέζιο (επειδή εγγράφεται) και επομένως  και κατ' επέκταση
και κατ' επέκταση  . Προφανώς
. Προφανώς  παραλληλόγραμμα. Δίδεται ότι:
παραλληλόγραμμα. Δίδεται ότι: . Διαρώντας με το
. Διαρώντας με το  παίρνουμε την ισοδύναμη:
παίρνουμε την ισοδύναμη:  .
. έχουμε: μια πλευρά ίση
έχουμε: μια πλευρά ίση  , μια γωνία ίση
, μια γωνία ίση  και το άθροισμα των δύο άλλων πλευρών ίσο.
και το άθροισμα των δύο άλλων πλευρών ίσο.  όπου γνωρίζουμε τα εξής δεδομένα: Την πλευρά
όπου γνωρίζουμε τα εξής δεδομένα: Την πλευρά  , την γωνία
, την γωνία  και το
και το  .
. Ωραία σκέψηAltrian έγραψε: ↑Πέμ Αύγ 16, 2018 7:48 pmΚαλησπέρα. Σκέφτηκα μια διαφορετική προσέγγιση και θα ήθελα να την εκθέσω.
Εστωτο μέσο της
, όπου δηλ. τέμνονται και οι
και
. Εστω επίσης
τα μέσα των
αντίστοιχα.
Εχουμε ότικαι
. Αρα
. Αρα
ισοσκελές τραπέζιο (επειδή εγγράφεται) και επομένως
και κατ' επέκταση
. Προφανώς
παραλληλόγραμμα. Δίδεται ότι:
. Διαρώντας με το
παίρνουμε την ισοδύναμη:
.
Ετσι για ταέχουμε: μια πλευρά ίση
, μια γωνία ίση
και το άθροισμα των δύο άλλων πλευρών ίσο.
Η απόδειξη επομένως ανάγεται στην δυνατότητα κατασκευής (μονοσήμαντα) τριγώνου, έστωόπου γνωρίζουμε τα εξής δεδομένα: Την πλευρά
, την γωνία
και το
.
Ο συγκεκριμένος ισχυρισμός (δυνατότητα μονοσήμαντης κατασκευής τριγώνου) ισχύει, άρα τα τρίγωνα είναι ίσα. Η απόδειξη της κατασκευής είναι απλή και όμορφη.
Θα ήθελα την γνώμη σας αν θα πρέπει να παρουσιαστεί εδώ, ή αν πρέπει να αποτελέσει αντικείμενο ανεξάρτητης άσκησης, ή αν έχει παρουσιαστεί στο παρελθόν στο forum, οπότε να γίνει αναφορά.
 έστω
έστω  , καθώς και το άθροισμα των δύο άλλων πλευρών. Αρα γνωρίζουμε την περίμετρο του υπό κατασκευή τριγώνου και έστω
, καθώς και το άθροισμα των δύο άλλων πλευρών. Αρα γνωρίζουμε την περίμετρο του υπό κατασκευή τριγώνου και έστω 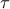 η ημιπερίμετρος.
η ημιπερίμετρος. δημιουργώ την δεδομένη γωνία
δημιουργώ την δεδομένη γωνία 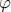 και ορίζω τμήματα
και ορίζω τμήματα  . Από τα
. Από τα 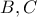 φέρνω τις καθέτους στις
φέρνω τις καθέτους στις  αντίστοιχα που τέμνονται στο
αντίστοιχα που τέμνονται στο  . Ορίζω τον κύκλο
. Ορίζω τον κύκλο  . Πάνω στην
. Πάνω στην  παίρνω το γνωστό τμήμα
παίρνω το γνωστό τμήμα  ίσο δηλ. με την γνωστή πλευρά. Από το
ίσο δηλ. με την γνωστή πλευρά. Από το  φέρνω την εφαπτομένη του κύκλου
φέρνω την εφαπτομένη του κύκλου που εφάπτεται έστω στο
που εφάπτεται έστω στο  και τέμνει την
και τέμνει την  έστω στο
έστω στο  .
.
 ολοκληρώθηκε.
ολοκληρώθηκε. Κατασκευάζω το τρίγωνο
Κατασκευάζω το τρίγωνο  με
με  Η μεσοκάθετη του
Η μεσοκάθετη του  τέμνει την
τέμνει την  στην τρίτη κορυφή
στην τρίτη κορυφή  του ζητούμενου τριγώνου.
του ζητούμενου τριγώνου.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης