Σελίδα 1 από 1
Βρείτε το γινόμενο
Δημοσιεύτηκε: Τετ Απρ 04, 2018 6:16 pm
από george visvikis
Για τους θετικούς αριθμούς
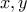
και

ισχύει ότι

Αν το άθροισμα των
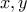
και

είναι

, να βρείτε το γινόμενό τους.
Re: Βρείτε το γινόμενο
Δημοσιεύτηκε: Σάβ Απρ 14, 2018 11:33 am
από george visvikis
Επαναφορά με υπόδειξη: Δείτε το γεωμετρικά.
Re: Βρείτε το γινόμενο
Δημοσιεύτηκε: Κυρ Απρ 15, 2018 12:31 pm
από Παύλος Μαραγκουδάκης
Είναι

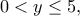

Υπάρχουν οξείες γωνίες

ώστε

Τότε
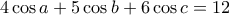
και

Θεωρούμε τους μιγαδικούς

Τότε

οπότε
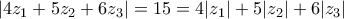
αφού

Άρα
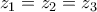
οπότε

και

Re: Βρείτε το γινόμενο
Δημοσιεύτηκε: Δευ Απρ 16, 2018 8:04 pm
από Ανδρέας Πούλος
Μια γεωμετρική λύση.
Κατασκευάζουμε ορθογώνιο τρίγωνο

με

,

,

.
Αυτή κατασκευή υπαγορεύεται από τα δεδομένα του προβλήματος και γίνεται κατανοητή στη συνέχεια.
Να παρατηρήσετε το συνημμένο σχήμα.
Ορίζω

και

, προκύπτει ότι

.
Ορίζω

και

, προκύπτει ότι

.
Ορίζω

και

, προκύπτει ότι

.
Στο συνημμένο σχήμα έχουμε παραλληλόγραμμα και όμοια τρίγωνα.
AB = 12 είναι το άθροισμα των τριών ριζών
BC = x + y + z = 9
AC = 4 + 5 + 6 = 15
Από τα όμοια τρίγωνα E

,

προκύπτει η αναλογία

Με όμοιο τρόπο, πάλι από τα όμοια τρίγωνα προκύπτει ότι
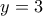
και

.

- x,y,zggb.png (15.74 KiB) Προβλήθηκε 1269 φορές
Re: Βρείτε το γινόμενο
Δημοσιεύτηκε: Δευ Απρ 16, 2018 11:38 pm
από george visvikis
Παύλο και Ανδρέα, σας ευχαριστώ για τις λύσεις. Η δική μου λύση είναι ίδια με του Ανδρέα.
Re: Βρείτε το γινόμενο
Δημοσιεύτηκε: Τρί Απρ 17, 2018 12:06 am
από S.E.Louridas
george visvikis έγραψε: ↑Τετ Απρ 04, 2018 6:16 pm
Για τους θετικούς αριθμούς
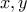
και

ισχύει ότι

Αν το άθροισμα των
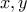
και

είναι

, να βρείτε το γινόμενό τους.
Ας δούμε και την εκδοχή που ακολουθεί και που είναι απλή εφαρμογή της ταυτότητας
Lagrange:
Για την λύση της άσκησης θεωρούμε

οπότε παίρνουμε

και

Αν υψώσουμε στο τετράγωνο τις σχέσεις αυτές έχουμε:

και

Αν τώρα θεωρήσουμε την ανάπτυξη των πρώτων μελών κατά τη ταυτότητα Lagrange

,
με το

να είναι άθροισμα τετραγώνων και προσθέσουμε κατά μέλη, θα πάρουμε

αφού θεωρούμε ως συντελεστές την μονάδα που εμφανίζεται

φορές επί το

μέσα λόγω των απλοποιήσεων κατά τη πρόσθεση που δίνει το
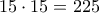
και που επίσης το
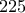
προκύπτει από την πρόσθεση αυτή και στο δεύτερο μέλος. Έτσι για το άθροισμα των τετραγώνων

που προκύπτει έχουμε

Eύκολα πλέον παίρνουμε

άρα και τις τιμές

. Οι τιμές αυτές επαληθεύουν τις εξισώσεις. Τελικά παίρνουμε
 (*)
(*) Υπενθυμίζουμε ότι η γενική μορφή της ταυτότητας του
Lagrange είναι:

 (**)
(**) Θεωρώ ότι θα επιλύεται και με θεώρηση κατάλληλων διανυσμάτων που τελικά βγαίνουν γραμμικώς εξαρτημένα έως ίσα, καθότι ήδη είδαμε την πανέμορφη λύση με μιγαδικούς του Παύλου.
Re: Βρείτε το γινόμενο
Δημοσιεύτηκε: Τρί Απρ 17, 2018 12:33 pm
από S.E.Louridas
S.E.Louridas έγραψε: ↑Τρί Απρ 17, 2018 12:06 am
george visvikis έγραψε: ↑Τετ Απρ 04, 2018 6:16 pm
Για τους θετικούς αριθμούς
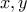
και

ισχύει ότι

Αν το άθροισμα των
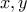
και

είναι

, να βρείτε το γινόμενό τους.
Ας δούμε και την εκδοχή που ακολουθεί και που είναι απλή εφαρμογή της ταυτότητας
Lagrange:
Για την λύση της άσκησης θεωρούμε

οπότε παίρνουμε

και

Αν υψώσουμε στο τετράγωνο τις σχέσεις αυτές έχουμε:

και

Αν τώρα θεωρήσουμε την ανάπτυξη των πρώτων μελών κατά τη ταυτότητα Lagrange

,
με το

να είναι άθροισμα τετραγώνων και προσθέσουμε κατά μέλη, θα πάρουμε

αφού θεωρούμε ως συντελεστές την μονάδα που εμφανίζεται

φορές επί το

μέσα λόγω των απλοποιήσεων κατά τη πρόσθεση που δίνει το
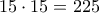
και που επίσης το
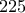
προκύπτει από την πρόσθεση αυτή και στο δεύτερο μέλος. Έτσι για το άθροισμα των τετραγώνων

που προκύπτει έχουμε

Eύκολα πλέον παίρνουμε

άρα και τις τιμές

. Οι τιμές αυτές επαληθεύουν τις εξισώσεις. Τελικά παίρνουμε
 (*)
(*) Υπενθυμίζουμε ότι η γενική μορφή της ταυτότητας του
Lagrange είναι:

 (**) Θεωρώ ότι θα επιλύεται και με θεώρηση κατάλληλων διανυσμάτων που τελικά βγαίνουν γραμμικώς εξαρτημένα έως ίσα, καθότι ήδη είδαμε την πανέμορφη λύση με μιγαδικούς του Παύλου
(**) Θεωρώ ότι θα επιλύεται και με θεώρηση κατάλληλων διανυσμάτων που τελικά βγαίνουν γραμμικώς εξαρτημένα έως ίσα, καθότι ήδη είδαμε την πανέμορφη λύση με μιγαδικούς του Παύλου.
(**) Πράγματι έχουμε και τη διαπραγμάτευση που ακολουθεί:


, που σημαίνει ότι θα υπάρχουν θετικοί

τέτοιοι που

και

Άρα παίρνουμε

και

οπότε

Όμοια έχουμε

και

οπότε
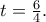
Έτσι οδηγούμαστε στις
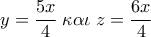
άρα

από όπου προκύπτoυν οι

και

τιμές που επαληθεύουν.
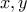 και
και  ισχύει ότι
ισχύει ότι 
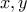 και
και  είναι
είναι  , να βρείτε το γινόμενό τους.
, να βρείτε το γινόμενό τους.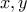 και
και  ισχύει ότι
ισχύει ότι 
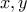 και
και  είναι
είναι  , να βρείτε το γινόμενό τους.
, να βρείτε το γινόμενό τους.
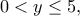

 ώστε
ώστε 
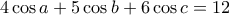


 οπότε
οπότε 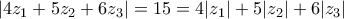 αφού
αφού 
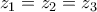 οπότε
οπότε  και
και 
 με
με  ,
,  ,
,  .
. και
και  , προκύπτει ότι
, προκύπτει ότι  .
. και
και  , προκύπτει ότι
, προκύπτει ότι  .
. και
και  , προκύπτει ότι
, προκύπτει ότι  .
. ,
, 
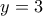 και
και .
.
 οπότε παίρνουμε
οπότε παίρνουμε  και
και 
 και
και 
 ,
,  να είναι άθροισμα τετραγώνων και προσθέσουμε κατά μέλη, θα πάρουμε
να είναι άθροισμα τετραγώνων και προσθέσουμε κατά μέλη, θα πάρουμε  αφού θεωρούμε ως συντελεστές την μονάδα που εμφανίζεται
αφού θεωρούμε ως συντελεστές την μονάδα που εμφανίζεται  φορές επί το
φορές επί το 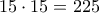 και που επίσης το
και που επίσης το 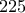 προκύπτει από την πρόσθεση αυτή και στο δεύτερο μέλος. Έτσι για το άθροισμα των τετραγώνων
προκύπτει από την πρόσθεση αυτή και στο δεύτερο μέλος. Έτσι για το άθροισμα των τετραγώνων  που προκύπτει έχουμε
που προκύπτει έχουμε 
 άρα και τις τιμές
άρα και τις τιμές 



 , που σημαίνει ότι θα υπάρχουν θετικοί
, που σημαίνει ότι θα υπάρχουν θετικοί  τέτοιοι που
τέτοιοι που  και
και 
 και
και  οπότε
οπότε 
 και
και  οπότε
οπότε 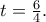 Έτσι οδηγούμαστε στις
Έτσι οδηγούμαστε στις 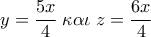 άρα
άρα  από όπου προκύπτoυν οι
από όπου προκύπτoυν οι  και
και  τιμές που επαληθεύουν.
τιμές που επαληθεύουν.