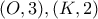 εφάπτονται εξωτερικά . Αναζητούνται όλα τα σημεία
εφάπτονται εξωτερικά . Αναζητούνται όλα τα σημεία  στο
στοεξωτερικό των δύο κύκλων , ώστε για τα εφαπτόμενα προς αυτούς τμήματα

να ισχύει :
 . Εντοπίστε εκείνο το
. Εντοπίστε εκείνο το  , για το οποίο είναι
, για το οποίο είναι  .
.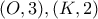 εφάπτονται εξωτερικά . Αναζητούνται όλα τα σημεία
εφάπτονται εξωτερικά . Αναζητούνται όλα τα σημεία  στο
στο
 . Εντοπίστε εκείνο το
. Εντοπίστε εκείνο το  , για το οποίο είναι
, για το οποίο είναι  .
.Μάλλον απλή για Ολυμπιάδες.
 με
με  , και δεδομένου ότι
, και δεδομένου ότι 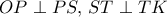 , η συνθήκη
, η συνθήκη  , γράφεται
, γράφεται ![(x^2+y^2)-3^2= 4[ (x-5)^2 + y^2 - 2^2] (x^2+y^2)-3^2= 4[ (x-5)^2 + y^2 - 2^2]](/forum/ext/geomar/texintegr/latexrender/pictures/bb7def9f1babdba9f328f3d401e70253.png) . Ισοδύναμα
. Ισοδύναμα  (κύκλος). Τα υπόλοιπα, άμεσα.
(κύκλος). Τα υπόλοιπα, άμεσα. ισοδυναμεί με
ισοδυναμεί με  , άρα
, άρα  , που μας δίνει εύκολα το
, που μας δίνει εύκολα το  ως τομή δύο κύκλων.
ως τομή δύο κύκλων.Μιχάλη ευχαριστώ για την ενασχόληση
Θανάση, ορθότατα.
Με Ευκλείδεια.
 το σημείο επαφής των κύκλων και
το σημείο επαφής των κύκλων και  οι διάμετροι των
οι διάμετροι των  αντίστοιχα. Η
αντίστοιχα. Η  τέμνει τους κύκλους κατά
τέμνει τους κύκλους κατά  Θέτω
Θέτω  οπότε
οπότε  και φέρνω από το
και φέρνω από το  κάθετη στην
κάθετη στην  που τέμνει την
που τέμνει την  στο
στο 
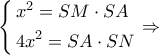


 και από την
και από την  προκύπτει ότι
προκύπτει ότι 

 Άρα η
Άρα η  είναι σταθερή κατά θέση και μέγεθος κι επειδή
είναι σταθερή κατά θέση και μέγεθος κι επειδή 

 τότε
τότε  και
και 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες