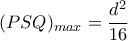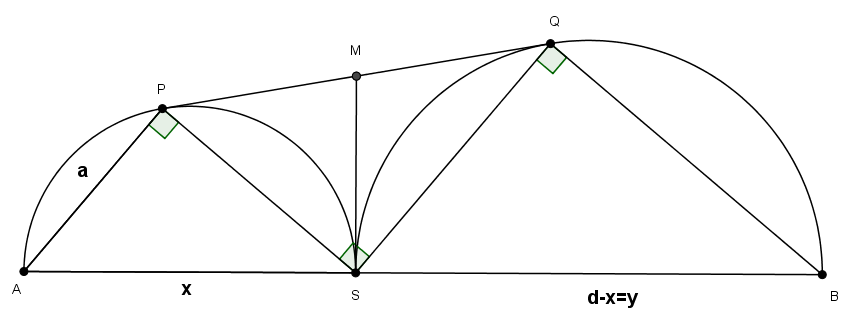
- Μεγιστοποίηση ορθογωνίου.png (21.72 KiB) Προβλήθηκε 1079 φορές
Φέρνουμε από το

την κοινή εφαπτόμενη των κύκλων και έστω πως τέμνει την

στο σημείο

.
Λόγω του ότι η
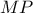
και η

είναι εφαπτόμενες στο ίδιο ημικύκλιο, έχουμε πως

. Όμοια έχουμε πως
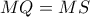
. Άρα
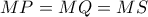
. Άρα πράγματι το τρίγωνο
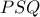
είναι ορθογώνιο.
Τα ορθογώνια τρίγωνα
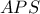
,
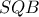
είναι όμοια, καθώς έχουν
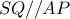
(

και
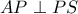
), άρα
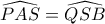
.
Λόγω του ότι
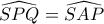
, έχουμε πως και το τρίγωνο
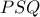
είναι όμοιο με τα
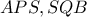
.
Έστω πως
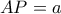
.
Θέτουμε για λόγους ευκολίας προς το παρόν πως
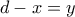
.
Έχουμε λοιπόν πως
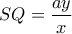
.
Ακόμη έχουμε από Πυθαγόρειο πως
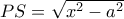
Έπεται λοιπόν πως
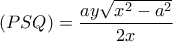
(1).
Επίσης έχουμε από Πυθαγόρειο πως
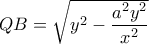
Άρα έχουμε πως
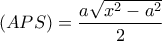
(2) και πως

(3)
Από τις (1), (2) και (3) φτάνουμε μετά από πράξεις στο ότι
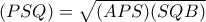
.
Λόγω τώρα του ότι τα τρία αυτά τρίγωνα είναι όμοια έχουμε μετά από πράξεις και πως
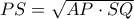
.
Άρα
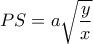
.
Ταυτόχρονα όμως
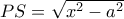
.
Συνεπώς
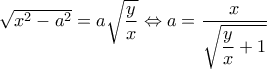
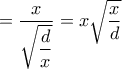
.
Επομένως
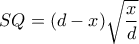
,

, άρα

.
Αφού το

είναι σταθερό, η μέγιστη τιμή του

επιτυγχάνεται όταν μεγιστοποιείται το

, δηλαδή όταν μεγιστοποιείται το
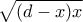
. Αφού όμως το άθροισμα
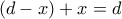
είναι σταθερό, από

έχουμε πως το
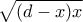
μεγιστοποιείται όταν
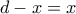
.
Άρα το μέγιστο εμβαδόν είναι

και επιτυγχάνεται όταν το

είναι το μέσο του

.
 κινείται στο εσωτερικό τμήματος
κινείται στο εσωτερικό τμήματος  . Σχεδιάζουμε στο ίδιο ημιεπίπεδο τα
. Σχεδιάζουμε στο ίδιο ημιεπίπεδο τα και φέρουμε το κοινό τους εξωτερικά εφαπτόμενο τμήμα
και φέρουμε το κοινό τους εξωτερικά εφαπτόμενο τμήμα  .
. είναι ορθογώνιο , υπολογίστε το εμβαδόν του συναρτήσει του
είναι ορθογώνιο , υπολογίστε το εμβαδόν του συναρτήσει του 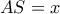 και βρείτε τη μέγιστη τιμή που μπορεί να λάβει αυτό το εμβαδόν .
και βρείτε τη μέγιστη τιμή που μπορεί να λάβει αυτό το εμβαδόν .
 .
.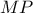 και η
και η  είναι εφαπτόμενες στο ίδιο ημικύκλιο, έχουμε πως
είναι εφαπτόμενες στο ίδιο ημικύκλιο, έχουμε πως  . Όμοια έχουμε πως
. Όμοια έχουμε πως 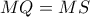 . Άρα
. Άρα 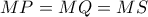 . Άρα πράγματι το τρίγωνο
. Άρα πράγματι το τρίγωνο 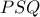 είναι ορθογώνιο.
είναι ορθογώνιο.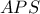 ,
, 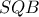 είναι όμοια, καθώς έχουν
είναι όμοια, καθώς έχουν 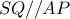 (
( και
και 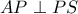 ), άρα
), άρα 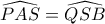 .
.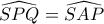 , έχουμε πως και το τρίγωνο
, έχουμε πως και το τρίγωνο 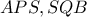 .
.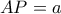 .
.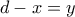 .
.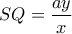 .
.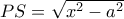
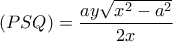 (1).
(1).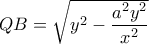
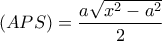 (2) και πως
(2) και πως  (3)
(3)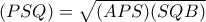 .
.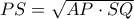 .
. 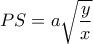 .
.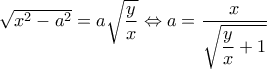
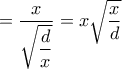 .
.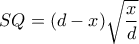 ,
,  , άρα
, άρα  .
. είναι σταθερό, η μέγιστη τιμή του
είναι σταθερό, η μέγιστη τιμή του  επιτυγχάνεται όταν μεγιστοποιείται το
επιτυγχάνεται όταν μεγιστοποιείται το  , δηλαδή όταν μεγιστοποιείται το
, δηλαδή όταν μεγιστοποιείται το 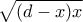 . Αφού όμως το άθροισμα
. Αφού όμως το άθροισμα 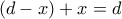 είναι σταθερό, από
είναι σταθερό, από  έχουμε πως το
έχουμε πως το 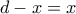 .
.  και επιτυγχάνεται όταν το
και επιτυγχάνεται όταν το  .
. τα κέντρα των ημικυκλίων και
τα κέντρα των ημικυκλίων και 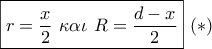 οι ακτίνες τους.
οι ακτίνες τους.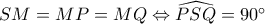 .
. το ύψος προς την υποτείνουσα στο
το ύψος προς την υποτείνουσα στο  θα είναι :
θα είναι :  .
.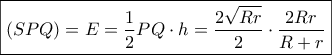 Που λόγω των σχέσεων
Που λόγω των σχέσεων  γίνεται
γίνεται  , παρουσιάζει δε μέγιστο για
, παρουσιάζει δε μέγιστο για 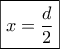 το
το 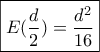 .
. με σταθερή υποτείνουσα
με σταθερή υποτείνουσα 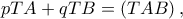 οπότε το γινόμενο
οπότε το γινόμενο 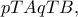 άρα και το
άρα και το 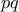 δηλαδή το εμβαδόν
δηλαδή το εμβαδόν  γίνεται μέγιστο όταν
γίνεται μέγιστο όταν 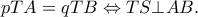 Όμως το μέγιστο από τα ορθογώνια τρίγωνα
Όμως το μέγιστο από τα ορθογώνια τρίγωνα  ταυτιστεί με το μέσο
ταυτιστεί με το μέσο  του ημικυκλίου
του ημικυκλίου 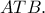 Τότε το μέγιστο
Τότε το μέγιστο  το έχουμε όταν
το έχουμε όταν 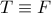 δηλαδή όταν
δηλαδή όταν 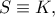 όπου
όπου  είναι το μέσον της διαμέτρου
είναι το μέσον της διαμέτρου  Και έτσι φτάσαμε σε μία ακόμη απάντηση.
Και έτσι φτάσαμε σε μία ακόμη απάντηση.
 σταθερό
σταθερό  σταθερό
σταθερό 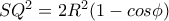 και
και 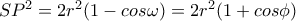 ,
, 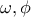 είναι παραπληρωματικές . Πολλαπλασιάζοντας παίρνουμε :
είναι παραπληρωματικές . Πολλαπλασιάζοντας παίρνουμε :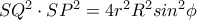 δηλαδή :
δηλαδή : 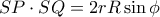 . Τελικά :
. Τελικά :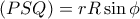 το οποίο μεγιστοποιείται αν μεγιστοποιηθεί το
το οποίο μεγιστοποιείται αν μεγιστοποιηθεί το 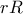 και το
και το 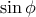 .
.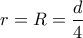 (αφού
(αφού 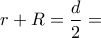 σταθερό ) και τότε
σταθερό ) και τότε