 το έγκεντρο τριγώνου
το έγκεντρο τριγώνου  με
με  Να βρεθούν οι πλευρές
Να βρεθούν οι πλευρές  αν γνωρίζουμε ότι αποτελούν
αν γνωρίζουμε ότι αποτελούν (με τη σειρά που δίνονται) γνησίως αύξουσα αριθμητική πρόοδο με θετικούς και ακέραιους όρους.
 το έγκεντρο τριγώνου
το έγκεντρο τριγώνου  με
με  Να βρεθούν οι πλευρές
Να βρεθούν οι πλευρές  αν γνωρίζουμε ότι αποτελούν
αν γνωρίζουμε ότι αποτελούν  .
. είναι όροι αριθμητικής προόδου, άρα
είναι όροι αριθμητικής προόδου, άρα  .
. , οπότε
, οπότε  , και αφού
, και αφού  , είναι
, είναι  , και άρα
, και άρα  .
. .
. προκύπτει
προκύπτει  .
. .
. , και
, και  .
.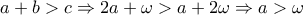 (2).
(2). (3).
(3). (4).
(4). (5).
(5). και τελικά
και τελικά  .
.Πολύ ωραία ΟρέστηΟρέστης Λιγνός έγραψε:Έστω.
Οιείναι όροι αριθμητικής προόδου, άρα
.
Είναι, οπότε
, και αφού
, είναι
, και άρα
.
Όμως είναι γνωστό ότι (αποδεικνύεται εύκολα με διαδοχική εφαρμογή του Ν. Συνημιτόνων).
Από τηνπροκύπτει
.
Όμως,.
Έστω τώρα, και
.
Επίσης,(2).
Έτσι,(3).
Ακόμη,(4).
Επίσης,(5).
Από (3), (4),(5) προκύπτει ότικαι τελικά
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες