 η διάμεσος
η διάμεσος  , τέμνει τον έγκυκλο στα σημεία
, τέμνει τον έγκυκλο στα σημεία  . Υπολογίστε το μήκος της χορδής
. Υπολογίστε το μήκος της χορδής  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 η διάμεσος
η διάμεσος  , τέμνει τον έγκυκλο στα σημεία
, τέμνει τον έγκυκλο στα σημεία  . Υπολογίστε το μήκος της χορδής
. Υπολογίστε το μήκος της χορδής  .
.Η ημιπερίμετρος του
 είναι
είναι  . Επειδή (π.χ.)
. Επειδή (π.χ.)  .
. 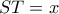 Επειδή το
Επειδή το  είναι ισοσκελές τραπέζιο θα είναι :
είναι ισοσκελές τραπέζιο θα είναι :  οπότε :
οπότε :  .
. προκύπτει ,
προκύπτει , και αφού ,
και αφού , θα ισχύουν ταυτόχρονα :
θα ισχύουν ταυτόχρονα :
 και επειδή το
και επειδή το 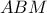 είναι ισοσκελές, η
είναι ισοσκελές, η 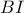 είναι μεσοκάθετη του
είναι μεσοκάθετη του  άρα οι
άρα οι 
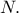 Από τον τύπο της διαμέσου παίρνω
Από τον τύπο της διαμέσου παίρνω  και με Π. Θ στο
και με Π. Θ στο  είναι
είναι 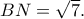 Από την ομοιότητα των τριγώνων
Από την ομοιότητα των τριγώνων  είναι
είναι 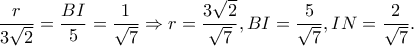



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 19 επισκέπτες