 είναι μεσοκάθετη της διαμέτρου
είναι μεσοκάθετη της διαμέτρου  ενός ημικυκλίου . Σημείο
ενός ημικυκλίου . Σημείο 
κινείται στο τόξο
 . Η
. Η  τέμνει την
τέμνει την  στο
στο  . Η κάθετη προς την
. Η κάθετη προς την  στο
στο  ,
, τέμνει την εφαπτομένη του ημικυκλίου στο
 , στο σημείο
, στο σημείο  . Υπολογίστε το τμήμα
. Υπολογίστε το τμήμα 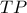 .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι μεσοκάθετη της διαμέτρου
είναι μεσοκάθετη της διαμέτρου  ενός ημικυκλίου . Σημείο
ενός ημικυκλίου . Σημείο 
 . Η
. Η  τέμνει την
τέμνει την  στο
στο  . Η κάθετη προς την
. Η κάθετη προς την  στο
στο  ,
,  , στο σημείο
, στο σημείο  . Υπολογίστε το τμήμα
. Υπολογίστε το τμήμα 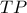 .
.
 είναι εγράψιμο αφού
είναι εγράψιμο αφού 
 είναι ισοσκελές τραπέζιο και
είναι ισοσκελές τραπέζιο και 
 Τότε ισχύουν οι παρακάτω ισότητες γωνιών:
Τότε ισχύουν οι παρακάτω ισότητες γωνιών:



 παίρνουμε
παίρνουμε 
 παίρνουμε
παίρνουμε 
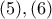 προκύπτει ότι
προκύπτει ότι 
 λαμβάνουμε
λαμβάνουμε  , άρα τελικά
, άρα τελικά  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες