 με περίκεντρο
με περίκεντρο  . Θεωρούμε ευθεία που διέρχεται από το
. Θεωρούμε ευθεία που διέρχεται από το  και τέμνει τον περίκυκλο του τριγώνου
και τέμνει τον περίκυκλο του τριγώνου  στα σημεία
στα σημεία 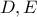 (το
(το  στο εσωτερικό του
στο εσωτερικό του  ), έτσι ώστε
), έτσι ώστε 
Αν
 τα μέσα των
τα μέσα των  αντίστοιχα, να αποδείξετε ότι το τετράπλευρο
αντίστοιχα, να αποδείξετε ότι το τετράπλευρο 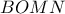 είναι εγγράψιμο και να υπολογίσετε τον λόγο
είναι εγγράψιμο και να υπολογίσετε τον λόγο 

 η ακτίνα του κύκλου.
η ακτίνα του κύκλου.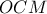 από τα δεδομένα (η χορδή
από τα δεδομένα (η χορδή  , γιατί έχει αντίστοιχη εγγεγραμμένη γωνία
, γιατί έχει αντίστοιχη εγγεγραμμένη γωνία  και η
και η 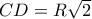 , γιατί έχει αντίστοιχη εγγεγραμμένη γωνία
, γιατί έχει αντίστοιχη εγγεγραμμένη γωνία  ):
):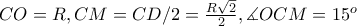 ,
, , οπότε
, οπότε 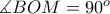 .
. είναι κάθετη στην
είναι κάθετη στην  , που θα δώσει
, που θα δώσει  . Σε συνδυασμό με την
. Σε συνδυασμό με την  είναι συζυγείς αρμονικές των ακτίνων
είναι συζυγείς αρμονικές των ακτίνων  είναι η πολική του
είναι η πολική του  . Θα βρούμε την εφαπτομένη της. Έχουμε τον διπλό λόγο:
. Θα βρούμε την εφαπτομένη της. Έχουμε τον διπλό λόγο:
 , εμφανίζoυμε την
, εμφανίζoυμε την  και την βρίσκουμε
και την βρίσκουμε
 και επειδή
και επειδή  η
η  Η εγγραψιμότητα του τετραπλεύρου
Η εγγραψιμότητα του τετραπλεύρου  δηλαδή ισχύει το εξής γενικότερο πρόβλημα:
δηλαδή ισχύει το εξής γενικότερο πρόβλημα:  και τυχούσα τέμνουσα
και τυχούσα τέμνουσα 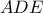 του περίκυκλου
του περίκυκλου  του τριγώνου
του τριγώνου  (με
(με  . Να δειχτεί ότι τα σημεία
. Να δειχτεί ότι τα σημεία  είναι ομοκυκλικά, όπου
είναι ομοκυκλικά, όπου  με
με  διέρχεται και από το μέσο
διέρχεται και από το μέσο  της
της  που ταυτίζεται με το σημείο τομής της
που ταυτίζεται με το σημείο τομής της  με την
με την  (λόγω του ισοπλεύρου τριγώνου
(λόγω του ισοπλεύρου τριγώνου  είναι (προφανώς) εφαπτόμενη του κύκλου
είναι (προφανώς) εφαπτόμενη του κύκλου 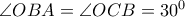 ) και συνεπώς
) και συνεπώς 

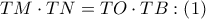
 σύμφωνα με το αντίστροφο του θεωρήματος των τεμνομένων χορδών προκύπτει η ομοκυκλικότητα των σημείων
σύμφωνα με το αντίστροφο του θεωρήματος των τεμνομένων χορδών προκύπτει η ομοκυκλικότητα των σημείων 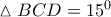 όπως αναφέρει το Κώστας πιο πάνω προκύπτει ότι η
όπως αναφέρει το Κώστας πιο πάνω προκύπτει ότι η  είναι διάμετρος του περίκυκλου του εγγραψίμου τετραπλεύρου
είναι διάμετρος του περίκυκλου του εγγραψίμου τετραπλεύρου  (ή καλύτερα της έκφρασης του
(ή καλύτερα της έκφρασης του  συναρτήσει της πλευράς
συναρτήσει της πλευράς  του ισοπλεύρου τριγώνου
του ισοπλεύρου τριγώνου