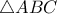 εφάπτεται των πλευρών
εφάπτεται των πλευρών  ,
,  ,
,  στα σημεία
στα σημεία  ,
,  ,
,  , αντίστοιχα.
, αντίστοιχα. Θεωρούμε σημείο
 στην ευθεία
στην ευθεία  τέτοιο ώστε
τέτοιο ώστε  , και η
, και η  τέμνει για δεύτερη φορά τον εγγεγραμμένο
τέμνει για δεύτερη φορά τον εγγεγραμμένο κύκλο του
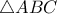 στο σημείο
στο σημείο  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
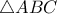 εφάπτεται των πλευρών
εφάπτεται των πλευρών  ,
,  ,
,  στα σημεία
στα σημεία  ,
,  ,
,  , αντίστοιχα.
, αντίστοιχα.  στην ευθεία
στην ευθεία  τέτοιο ώστε
τέτοιο ώστε  , και η
, και η  τέμνει για δεύτερη φορά τον εγγεγραμμένο
τέμνει για δεύτερη φορά τον εγγεγραμμένο 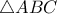 στο σημείο
στο σημείο  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.
 το μέσο της
το μέσο της  . Ισχύει
. Ισχύει  (ως εφαπτόμενα τμήματα) άρα το τρίγωνο
(ως εφαπτόμενα τμήματα) άρα το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές.  είναι και ύψος. Άρα
είναι και ύψος. Άρα  Έτσι αρκεί να αποδείξουμε ότι το τετράπλευρο
Έτσι αρκεί να αποδείξουμε ότι το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο. είναι αρμονικό. Άρα η
είναι αρμονικό. Άρα η  είναι συμμετροδιάμεσος στο τρίγωνο
είναι συμμετροδιάμεσος στο τρίγωνο  και η
και η  διάμεσος, άρα
διάμεσος, άρα 
 .
.  .
.  και
και  είναι όμοια, άρα
είναι όμοια, άρα  (χορδής - εφαπτομένης)
(χορδής - εφαπτομένης)  (από την παραλληλία) και το ζητούμενο έπεται.
(από την παραλληλία) και το ζητούμενο έπεται. 
Η διάμετροςgiannimani έγραψε: ↑Τετ Ιούλ 06, 2022 10:37 amΟ εγγεγραμμένος κύκλος τουεφάπτεται των πλευρών
,
,
στα σημεία
,
,
, αντίστοιχα.
Θεωρούμε σημείοστην ευθεία
τέτοιο ώστε
, και η
τέμνει για δεύτερη φορά τον εγγεγραμμένο
κύκλο τουστο σημείο
. Να αποδείξετε ότι
.
probl_right.png
 τέμνει την
τέμνει την  στο
στο  και προφανώς
και προφανώς  ομοκυκλικά
ομοκυκλικά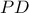 κόψει τον εγγεγραμμένο κύκλο στο
κόψει τον εγγεγραμμένο κύκλο στο  ,τότε
,τότε  ομοκυκλικά και οι κόκκινες γωνίες είναι ίσες
ομοκυκλικά και οι κόκκινες γωνίες είναι ίσες άρα
άρα  ομοκυκλικά ,συνεπώς
ομοκυκλικά ,συνεπώς  συνευθειακά και
συνευθειακά και 
Προφανώς το τετράπλευροgiannimani έγραψε: ↑Τετ Ιούλ 06, 2022 10:37 amΟ εγγεγραμμένος κύκλος τουεφάπτεται των πλευρών
,
,
στα σημεία
,
,
, αντίστοιχα.
Θεωρούμε σημείοστην ευθεία
τέτοιο ώστε
, και η
τέμνει για δεύτερη φορά τον εγγεγραμμένο
κύκλο τουστο σημείο
. Να αποδείξετε ότι
.
probl_right.png
 είναι αρμονικό. Ας είναι
είναι αρμονικό. Ας είναι  το σημείο τομής των διαγωνίων του και
το σημείο τομής των διαγωνίων του και  τα σημεία τομής των
τα σημεία τομής των  με τη
με τη  .
Η δέσμη :
.
Η δέσμη :  είναι αρμονική κι αφού η ευθεία
είναι αρμονική κι αφού η ευθεία  είναι παράλληλη στην ακτίνα,
είναι παράλληλη στην ακτίνα,  , της δέσμης, θα είναι
, της δέσμης, θα είναι  .
.  είναι κι αυτή εφαπτομένη του κύκλου( λόγω του αρμονικού τετραπλεύρου) και άρα :
είναι κι αυτή εφαπτομένη του κύκλου( λόγω του αρμονικού τετραπλεύρου) και άρα : 
 το αντιδιαμετρικό του
το αντιδιαμετρικό του  , και
, και  το δεύτερο σημείο τομής της
το δεύτερο σημείο τομής της  με τον κύκλο
με τον κύκλο  .
. το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  , και με
, και με  το σημείο τομής
το σημείο τομής  και
και  . Στο τρίγωνο
. Στο τρίγωνο  τα
τα  ,
,  είναι ύψη του τριγώνου,
είναι ύψη του τριγώνου,  . Επομένως, το σημείο τομής των
. Επομένως, το σημείο τομής των  είναι ορθόκεντρο
είναι ορθόκεντρο  . Εφόσον
. Εφόσον  , τότε
, τότε  .
. διέρχεται από το
διέρχεται από το  , οπότε
, οπότε  .
. ,
,  ,
,  είναι αντίστοιχα οι ριζικοί άξονες των ζευγών των κύκλων
είναι αντίστοιχα οι ριζικοί άξονες των ζευγών των κύκλων  και
και  ,
,  και
και  ,
,  και
και  (οι τρεις κύκλοι τέμνονται ανά δύο). Επομένως, διέρχονται από το ίδιο σημείο.
(οι τρεις κύκλοι τέμνονται ανά δύο). Επομένως, διέρχονται από το ίδιο σημείο.



 το μέσον της
το μέσον της 
 , που ισχύει λόγο αρμονικού τετραπλεύρου.
, που ισχύει λόγο αρμονικού τετραπλεύρου. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες