giannimani έγραψε: ↑Σάβ Μάιος 07, 2022 10:27 am
right_angle.pngΑπό ένα σημείο

, που βρίσκεται εκτός ενός δεδομένου κύκλου, φέρουμε δύο τέμνουσες του κύκλου. Η μια απ' αυτές διέρχεται από το κέντρο

του κύκλου και τον τέμνει στα σημεία

και

. Η δεύτερη τέμνουσα τέμνει τον κύκλο στα σημεία

και

. Οι περιγεγραμμένοι κύκλοι των τριγώνων

και

, τέμνονται για δεύτερη φορά στο σημείο

.
Να αποδείξετε ότι

Μια ακόμη λύση. Τώρα με αντιστροφή .
Θεωρώ πόλο το κέντρο

και δύναμη αντιστροφής την ακτίνα του

, δηλαδή κύκλος αντιστροφής είναι ο

.
Αντιστρέφω πρώτα τον κύκλο

και δίδει εικόνα την ευθεία

( Στο

από την συμμετρία ως προς κύκλο δείχνω πρώτα τον κύκλο

και μετά τον

και θα σχεδιαστεί άμεσα η ευθεία

, όμοια και για τις άλλες αντιστροφές )
Ομοίως ο

. Οι ευθείες τέμνονται στο

, αφού δε οι κύκλοι
τέμνονται στο

η εικόνα του

είναι το

και τα σημεία

(πόλος) και τα

είναι συνευθειακά .
θα ισχύει:


- Εμφάνιση ορθής_2.png (24.69 KiB) Προβλήθηκε 552 φορές
Πάλι με πόλο το

και κύκλο αντιστροφής τον

η εικόνα της ευθείας

θα είναι κύκλος γιατί αυτή η τέμνουσα δεν διέρχεται από τον πόλο

.
Αναγκαστικά αυτός ο κύκλος θα διέρχεται από το

και από τα σημεία

. Δηλαδή :

Ο πιο πάνω κύκλος θα τέμνει ακόμα την διάμετρο

σε ένα σημείο έστω

. Ας πούμε τώρα

το σημείο τομής των

.
Για το τρίγωνο
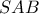
τα σημεία

είναι οι πόδες των υψών ενώ το

είναι μέσο της

,
ο κύκλος

είναι ο κύκλος

του
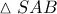
οπότε το

είναι ο πόδας του ύψους από το

.
Εικόνα του

στην αντιστροφή της ευθείας

είναι το

με άμεση συνέπεια ,

Από τις

προκύπτει ότι το τετράπλευρο

είναι εγγράψιμο και προφανώς οι γωνίες του στα

θα είναι παραπληρωματικές , άρα

 , που βρίσκεται εκτός ενός δεδομένου κύκλου, φέρουμε δύο τέμνουσες του κύκλου. Η μια απ' αυτές διέρχεται από το κέντρο
, που βρίσκεται εκτός ενός δεδομένου κύκλου, φέρουμε δύο τέμνουσες του κύκλου. Η μια απ' αυτές διέρχεται από το κέντρο  του κύκλου και τον τέμνει στα σημεία
του κύκλου και τον τέμνει στα σημεία  και
και  . Η δεύτερη τέμνουσα τέμνει τον κύκλο στα σημεία
. Η δεύτερη τέμνουσα τέμνει τον κύκλο στα σημεία  και
και  . Οι περιγεγραμμένοι κύκλοι των τριγώνων
. Οι περιγεγραμμένοι κύκλοι των τριγώνων  και
και  , τέμνονται για δεύτερη φορά στο σημείο
, τέμνονται για δεύτερη φορά στο σημείο  .
. 

 το σημείο τομής των
το σημείο τομής των  , η δε
, η δε  τέμνει τον κύκλο
τέμνει τον κύκλο  στο
στο  .
. τα σημεία
τα σημεία  καθώς και τα σημεία
καθώς και τα σημεία  είναι ομοκυκλικά .
είναι ομοκυκλικά .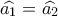 ( βαίνουν σε ίσα τόξα) έτσι από το έμμεσο κριτήριο ισότητας τριγώνων θα έχω:
( βαίνουν σε ίσα τόξα) έτσι από το έμμεσο κριτήριο ισότητας τριγώνων θα έχω:  και άρα το τετράπλευρο
και άρα το τετράπλευρο  είναι χαρταετός .
είναι χαρταετός .
 . Αλλά
. Αλλά  , άρα
, άρα  .
. κι αφού
κι αφού  έχω:
έχω: 
 ως το ριζικό κέντρο των ανά δύο τεμνομένων κύκλων
ως το ριζικό κέντρο των ανά δύο τεμνομένων κύκλων  και ας είναι
και ας είναι  Με
Με 
 ομοκυκλικά (έστω σε κύκλο
ομοκυκλικά (έστω σε κύκλο  ) και με
) και με  εφαπτόμενη του
εφαπτόμενη του  η δεύτερη από το
η δεύτερη από το  η πολική του
η πολική του  είναι αρμονική και συνεπώς και η δέσμη
είναι αρμονική και συνεπώς και η δέσμη  είναι αρμονική, άρα και η σειρά
είναι αρμονική, άρα και η σειρά  είναι αρμονική και συνεπώς και η δέσμη
είναι αρμονική και συνεπώς και η δέσμη  είναι αρμονική και με
είναι αρμονική και με  διχοτόμος της
διχοτόμος της 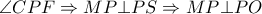 και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί .  η τομή των ευθειών
η τομή των ευθειών  και
και  . Τότε, στο τρίγωνο
. Τότε, στο τρίγωνο  τα
τα  ,
,  είναι ύψη
είναι ύψη  είναι το ορθόκεντρο του τριγώνου.
είναι το ορθόκεντρο του τριγώνου. τέμνει την
τέμνει την  στο
στο  , τότε
, τότε  .
. . Ως εκ τούτου, το
. Ως εκ τούτου, το  .
. είναι εγγράψιμο, ή
είναι εγγράψιμο, ή  .
. (εγγεγραμμένες γωνίες του κύκλου
(εγγεγραμμένες γωνίες του κύκλου που βαίνουν σε τόξα των ίσων χορδών
που βαίνουν σε τόξα των ίσων χορδών  ,
,  ). Από το εγγεγραμμένο στον κύκλο
). Από το εγγεγραμμένο στον κύκλο  έχουμε
έχουμε  , οπότε λόγω της
, οπότε λόγω της 
 , και εφόσον
, και εφόσον  και
και  έχουν τη γωνία
έχουν τη γωνία  κοινή
κοινή  , είναι όμοια, δηλαδή,
, είναι όμοια, δηλαδή, .
. και
και  προκύπτει ότι
προκύπτει ότι  , δηλαδή το
, δηλαδή το  , τότε και
, τότε και  .
. ,
, 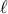 διέρχονται από ένα σημείο
διέρχονται από ένα σημείο  ), και τέμνουν
), και τέμνουν  στα σημεία
στα σημεία  ,
,  και
και  ,
,  , αντίστοιχα. Τότε,
, αντίστοιχα. Τότε,  ή
ή 
 η πολική του
η πολική του  , δηλαδή κύκλος αντιστροφής είναι ο
, δηλαδή κύκλος αντιστροφής είναι ο  .
. και δίδει εικόνα την ευθεία
και δίδει εικόνα την ευθεία  από την συμμετρία ως προς κύκλο δείχνω πρώτα τον κύκλο
από την συμμετρία ως προς κύκλο δείχνω πρώτα τον κύκλο  . Οι ευθείες τέμνονται στο
. Οι ευθείες τέμνονται στο  είναι συνευθειακά .
είναι συνευθειακά .
 θα είναι κύκλος γιατί αυτή η τέμνουσα δεν διέρχεται από τον πόλο
θα είναι κύκλος γιατί αυτή η τέμνουσα δεν διέρχεται από τον πόλο  . Δηλαδή :
. Δηλαδή : 
 το σημείο τομής των
το σημείο τομής των 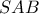 τα σημεία
τα σημεία  είναι οι πόδες των υψών ενώ το
είναι οι πόδες των υψών ενώ το  είναι ο κύκλος
είναι ο κύκλος  του
του 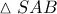 οπότε το
οπότε το 
 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο και προφανώς οι γωνίες του στα
είναι εγγράψιμο και προφανώς οι γωνίες του στα  θα είναι παραπληρωματικές , άρα
θα είναι παραπληρωματικές , άρα  και τοξ
και τοξ του κύκλου
του κύκλου  και
και  αντίστοιχα. Έχουμε
αντίστοιχα. Έχουμε  .
.  .
.  .
. , δηλαδή τα σημεία,
, δηλαδή τα σημεία,  ,
,  .
. 

 κι έτσι
κι έτσι  ομοκυκλικά
ομοκυκλικά 