Ας την προτείνω για να είμαι βέβαιος ότι κάποτε τέθηκε...
Την χρειάστηκα πρόσφατα για την απόδειξη μιας άλλης ανισότητας.
Σε τρίγωνο
 να αποδειχθεί ότι
να αποδειχθεί ότι
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 να αποδειχθεί ότι
να αποδειχθεί ότι
Θα χρησιμοποιήσω δύο γνωστές αλλά δύσκολες ανισότητες όμως δεν αμφιβάλω ότι θα υπάρχει ευκολότερος, πιο άμεσος τρόπος.
 και η άλλη είναι η Euler
και η άλλη είναι η Euler  .
.  που υπάρχει σε διάφορες παλιές Τριγωνομετρίες. Ο δεύτερος είναι η ιστορικά πρώτη ουσιαστική ανισότητα στα τρίγωνα, και την βρίσκει κανείς στην βιβλιογραφία.
που υπάρχει σε διάφορες παλιές Τριγωνομετρίες. Ο δεύτερος είναι η ιστορικά πρώτη ουσιαστική ανισότητα στα τρίγωνα, και την βρίσκει κανείς στην βιβλιογραφία. 


Nα ευχαριστήσω το Μιχάλη Λάμπρου για τη λύση που έγραψε.Mihalis_Lambrou έγραψε: ↑Πέμ Φεβ 17, 2022 9:36 pm
Τηλέμαχε, σου κάνουν αυτά ή έχεις κάτι πιο άμεσο και πονηρό;
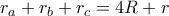


![\displaystyle E^{2}\left [ \frac{1}{\left ( s-a \right )\left ( s-b \right )} +\frac{1}{\left ( s-b \right )\left ( s-c \right )} +\frac{1}{\left ( s-c \right )\left ( s-a \right )} \right ]= \displaystyle E^{2}\left [ \frac{1}{\left ( s-a \right )\left ( s-b \right )} +\frac{1}{\left ( s-b \right )\left ( s-c \right )} +\frac{1}{\left ( s-c \right )\left ( s-a \right )} \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/0b31a2861a16c627f00ecd48a8050ec9.png)



Noμίζω ότι οφείλω να γράψω μια απόδειξη της ισότηταςΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Πέμ Φεβ 17, 2022 10:41 pmΔεν θεωρώ δεδομένο ότι ένας μαθητής της β' Λυκείου με ενδιαφέρον για τη Γεωμετρία τη γνωρίζει.
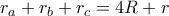 .
.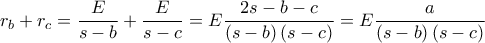


![\displaystyle Ea\left [ \frac{1}{\left ( s-b \right )\left ( s-c \right )}+\frac{1}{s\left ( s-a \right )} \right ]= \displaystyle Ea\left [ \frac{1}{\left ( s-b \right )\left ( s-c \right )}+\frac{1}{s\left ( s-a \right )} \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/43ca4acb4cd9c7c5c7809856246220f0.png)


 . Τότε
. Τότε  και
και 
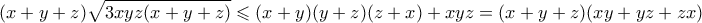
 θέτοντας
θέτοντας 
Ας παρατηρήσουμε ότι η ανισότητα αυτή είναι ουσιαστικά η Finsler-Hadwiger:ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Πέμ Φεβ 17, 2022 6:26 pmΤην παρακάτω ανισότητα είναι πολύ πιθανόν να την έχουμε ξαναδεί...
Ας την προτείνω για να είμαι βέβαιος ότι κάποτε τέθηκε...
Την χρειάστηκα πρόσφατα για την απόδειξη μιας άλλης ανισότητας.
Σε τρίγωνονα αποδειχθεί ότι


Aς δούμε την απόδειξη της παρατήρησης του Θάνου.matha έγραψε: ↑Παρ Φεβ 18, 2022 5:51 pmΑς παρατηρήσουμε ότι η ανισότητα αυτή είναι ουσιαστικά η Finsler-Hadwiger:ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Πέμ Φεβ 17, 2022 6:26 pmΤην παρακάτω ανισότητα είναι πολύ πιθανόν να την έχουμε ξαναδεί...
Ας την προτείνω για να είμαι βέβαιος ότι κάποτε τέθηκε...
Την χρειάστηκα πρόσφατα για την απόδειξη μιας άλλης ανισότητας.
Σε τρίγωνονα αποδειχθεί ότι





 (
( )
) .
. .
. ) είναι άμεση συνέπεια της ανισότητας
) είναι άμεση συνέπεια της ανισότητας  και της σχέσης
και της σχέσης
 το βαρύκεντρο του τριγώνου) :
το βαρύκεντρο του τριγώνου) : (1)
(1) (2)
(2) (3) βλέπε εδώ
(3) βλέπε εδώ η απόσταση των κέντρων του περιγεγραμμένου και εγγεγραμένου κύκλου του τριγώνου (σχέση του Euler). Από τις (1), (2), (3) προκύπτει η:
η απόσταση των κέντρων του περιγεγραμμένου και εγγεγραμένου κύκλου του τριγώνου (σχέση του Euler). Από τις (1), (2), (3) προκύπτει η: (4)
(4)  ), δεξί μέλος,
), δεξί μέλος, 
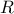 και κάνουμε την αντικατάσταση
και κάνουμε την αντικατάσταση  και η ανισότητα γίνεται
και η ανισότητα γίνεται
 στο διάστημα
στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) , αφού
, αφού  . Έχουμε
. Έχουμε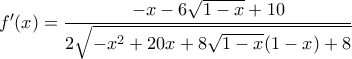


 και ο παραπάνω αριθμητής γίνεται
και ο παραπάνω αριθμητής γίνεται 


 και ειδικά στο διάστημα
και ειδικά στο διάστημα ![t \in [0,1] t \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/dff6e05ec00b53d46e366975136d0d2e.png) θα είναι
θα είναι  . Επομένως
. Επομένως 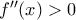 και η συνάρτηση
και η συνάρτηση  είναι κυρτή στο διάστημα
είναι κυρτή στο διάστημα ![x \in [0,1] x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) .
.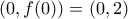 και
και  και την ευθεία
και την ευθεία  που διέρχεται από αυτά. Λόγω της παραπάνω κυρτότητας θα είναι:
που διέρχεται από αυτά. Λόγω της παραπάνω κυρτότητας θα είναι: που είναι πιο ισχυρή ανισότητα στην δημοσιεύση του Δημήτρη.
που είναι πιο ισχυρή ανισότητα στην δημοσιεύση του Δημήτρη.Παρατηρούμε μάλιστα ότι όχι μόνο είναι πιο ισχυρή αλλά και "βέλτιστη" δυνατή, αν περιοριστούμε σε ένα γραμμικό συνδιασμό των
 ως αναφορά την εκτίμηση προς τα πάνω της ημιπεριμέτρου. Δηλαδή για ανισότητες της μορφής
ως αναφορά την εκτίμηση προς τα πάνω της ημιπεριμέτρου. Δηλαδή για ανισότητες της μορφής .
.  , κτλ.
, κτλ.  στην παραπάνω μορφή είναι δική μου, στο πρωτότυπο υπάρχει διαφορετική μελέτη.
στην παραπάνω μορφή είναι δική μου, στο πρωτότυπο υπάρχει διαφορετική μελέτη. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες