
Έστω το σημείο

και έχουμε ότι η σημειοσειρά

, είναι αρμονική.
Γνωστό αποτέλεσμα το οποίο προκύπτει άμεσα από το πλήρες τετράπλευρο

, όπου

( δεν εμφανίζεται στο σχήμα ), ως το
Σημείο Gergone του δοσμένου τριγώνου

.
Έτσι, από
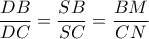
προκύπτει ότι τα ορθογώνια τρίγωνα

είναι όμοια
και επομένως ισχύει

Από

και




- Tran Quang Hung (Vietnam 2017).
- f=178 t=70636.PNG (27.65 KiB) Προβλήθηκε 1308 φορές

Έστω το σημείο

και από την αρμονική σημειοσειρά

στο τραπέζιο

έχουμε ότι το σημείο αυτό ανήκει στην ευθεία

, λόγω


.
Από
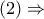

όπου

.
Από

, σύμφωνα με το
Θεώρημα Θαλή, προκύπτει άμεσα ότι οι δια των σημείων

παράλληλες ευθείες προς τις ευθείες

αντιστοίχως, τέμνουν την ευθεία

στο ίδιο σημείο, έστω το

.
Αλλά, σύμφωνα με το παρακάτω
Λήμμα, οι ίδιες ευθείες περνάνε από το μέσον του τμήματος

.
Συμπεραίνεται έτσι, ότι το σημείο

ταυτίζεται με το μέσον του

και το ζητούμενο έχει αποδειχθεί.

Η απόδειξη αυτή είναι αφιερωμένη σε ένδειξη τιμής, στον
Παναγιώτη Χρονόπουλο.
ΛΗΜΜΑ - Δίνεται ορθογώνιο τραπέζιο  με
με  και
και  και ας είναι
και ας είναι  . Έστω το σημείο
. Έστω το σημείο  και ας είναι
και ας είναι  η προβολή του
η προβολή του  επί της
επί της  . Αποδείξτε ότι οι δια των σημείων
. Αποδείξτε ότι οι δια των σημείων  παράλληλες ευθείες προς τις
παράλληλες ευθείες προς τις  αντιστοίχως, περνάνε από το μέσον της πλευράς
αντιστοίχως, περνάνε από το μέσον της πλευράς 
.
Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την απόδειξη που έχω υπόψη μου για το ως άνω
Λήμμα.
 στις κορυφές
στις κορυφές  τριγώνου
τριγώνου  τέμνουν την
τέμνουν την  στα σημεία
στα σημεία  αντίστοιχα , όπου
αντίστοιχα , όπου  τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του εν λόγω τριγώνου με τις πλευρές του
του εν λόγω τριγώνου με τις πλευρές του  αντίστοιχα και ας είναι
αντίστοιχα και ας είναι  τα σημεία τομής των
τα σημεία τομής των  με τον
με τον  αντίστοιχα, με
αντίστοιχα, με  και
και  . Να δείξετε ότι η
. Να δείξετε ότι η  διέρχεται από το μέσο της
διέρχεται από το μέσο της  , όπου
, όπου  .
.
 Έστω το σημείο
Έστω το σημείο  και έχουμε ότι η σημειοσειρά
και έχουμε ότι η σημειοσειρά  , είναι αρμονική.
, είναι αρμονική. , όπου
, όπου  ( δεν εμφανίζεται στο σχήμα ), ως το
( δεν εμφανίζεται στο σχήμα ), ως το 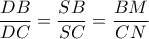 προκύπτει ότι τα ορθογώνια τρίγωνα
προκύπτει ότι τα ορθογώνια τρίγωνα  είναι όμοια
είναι όμοια
 και
και 


 και από την αρμονική σημειοσειρά
και από την αρμονική σημειοσειρά  έχουμε ότι το σημείο αυτό ανήκει στην ευθεία
έχουμε ότι το σημείο αυτό ανήκει στην ευθεία  , λόγω
, λόγω 
 .
.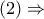
 όπου
όπου  .
. , σύμφωνα με το
, σύμφωνα με το  παράλληλες ευθείες προς τις ευθείες
παράλληλες ευθείες προς τις ευθείες  αντιστοίχως, τέμνουν την ευθεία
αντιστοίχως, τέμνουν την ευθεία  στο ίδιο σημείο, έστω το
στο ίδιο σημείο, έστω το  .
. με
με  και
και  και ας είναι
και ας είναι  . Έστω το σημείο
. Έστω το σημείο  και ας είναι
και ας είναι  η προβολή του
η προβολή του  επί της
επί της  . Αποδείξτε ότι οι δια των σημείων
. Αποδείξτε ότι οι δια των σημείων  παράλληλες ευθείες προς τις
παράλληλες ευθείες προς τις  αντιστοίχως, περνάνε από το μέσον της πλευράς
αντιστοίχως, περνάνε από το μέσον της πλευράς 
 , η προβολή του
, η προβολή του  , ως το σημείο τομής της
, ως το σημείο τομής της  παράλληλη ευθεία προς την
παράλληλη ευθεία προς την  και αρκεί να αποδειχθεί ότι το σημείο αυτό ταυτίζεται με το μέσον της
και αρκεί να αποδειχθεί ότι το σημείο αυτό ταυτίζεται με το μέσον της  και από
και από 

 , είναι αρμονική.
, είναι αρμονική. , τυχόν σημείο προς το μέρος της
, τυχόν σημείο προς το μέρος της  , ώστε να είναι
, ώστε να είναι  .
.
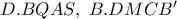 οι γωνίες που σχηματίζονται από τις ομόλογες ακτίνες τους είναι ίσες.
οι γωνίες που σχηματίζονται από τις ομόλογες ακτίνες τους είναι ίσες.
 και
και  και
και 

 είναι αρμονική λόγω της αρμονικής σημειοσειράς
είναι αρμονική λόγω της αρμονικής σημειοσειράς 
 είναι επίσης αρμονική και επομένως ισχύει
είναι επίσης αρμονική και επομένως ισχύει  λόγω
λόγω  .
. περνάει από το μέσον
περνάει από το μέσον  ώστε να είναι
ώστε να είναι  , όπου
, όπου  . Τότε με
. Τότε με 
 οπότε η από το
οπότε η από το  θα διέρχεται και από το μέσο
θα διέρχεται και από το μέσο  του τριγώνου
του τριγώνου  και ομοίως για την εκ του
και ομοίως για την εκ του  , με
, με  σημεία των
σημεία των  αντίστοιχα, ώστε
αντίστοιχα, ώστε  να δειχθεί ότι η
να δειχθεί ότι η  διέρχεται από το μέσο της
διέρχεται από το μέσο της  .
.
 και συνεπώς η σειρά
και συνεπώς η σειρά  είναι αρμονική , άρα και η δέσμη
είναι αρμονική , άρα και η δέσμη  είναι αρμονική και με
είναι αρμονική και με  το μέσο της
το μέσο της 
 προκύπτει ότι:
προκύπτει ότι: 

 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.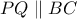 στο σχήμα της ανάρτησης #2 πιο πάνω.
στο σχήμα της ανάρτησης #2 πιο πάνω. , επομένως
, επομένως 
 άρα
άρα  και
και 

 η
η  γίνεται
γίνεται  από όπου έπεται το ζητούμενο.
από όπου έπεται το ζητούμενο.