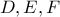 τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  ορθογωνίου στο
ορθογωνίου στο  τριγώνου
τριγώνου  με τις πλευρές του
με τις πλευρές του  αντίστοιχα. Να δειχθεί ότι ο περίκυκλος του τριγώνου
αντίστοιχα. Να δειχθεί ότι ο περίκυκλος του τριγώνου  διέρχεται από το
διέρχεται από το  , όπου
, όπου  τα ισοτομικά των
τα ισοτομικά των 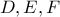 αντίστοιχα ως προς τις πλευρές που ανήκουν
αντίστοιχα ως προς τις πλευρές που ανήκουν Συντονιστές: vittasko, silouan, rek2
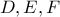 τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  ορθογωνίου στο
ορθογωνίου στο  τριγώνου
τριγώνου  με τις πλευρές του
με τις πλευρές του  αντίστοιχα. Να δειχθεί ότι ο περίκυκλος του τριγώνου
αντίστοιχα. Να δειχθεί ότι ο περίκυκλος του τριγώνου  διέρχεται από το
διέρχεται από το  , όπου
, όπου  τα ισοτομικά των
τα ισοτομικά των 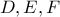 αντίστοιχα ως προς τις πλευρές που ανήκουν
αντίστοιχα ως προς τις πλευρές που ανήκουν ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Τετ Δεκ 01, 2021 2:55 pmΈστωτα σημεία επαφής του έγκυκλου
ορθογωνίου στο
τριγώνου
με τις πλευρές του
αντίστοιχα. Να δειχθεί ότι ο περίκυκλος του τριγώνου
διέρχεται από το
, όπου
τα ισοτομικά των
αντίστοιχα ως προς τις πλευρές που ανήκουν
 Έστω τα σημεία
Έστω τα σημεία  και
και  .
. έχουμε
έχουμε 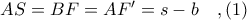 όπου
όπου  .
. και άρα, το τετράπλευρο
και άρα, το τετράπλευρο  είναι εγγράψιμο σε κύκλο έστω
είναι εγγράψιμο σε κύκλο έστω  , ως ισοσκελές τραπέζιο, λόγω των
, ως ισοσκελές τραπέζιο, λόγω των  .
. είναι εγγράψιμο.
είναι εγγράψιμο. όπου
όπου  .
. αρκεί
αρκεί  αρκεί
αρκεί 
 όμως αληθεύει λόγω του δοσμένου ορθογωνίου τριγώνου
όμως αληθεύει λόγω του δοσμένου ορθογωνίου τριγώνου  και επομένως το
και επομένως το  είναι εγγράψιμο.
είναι εγγράψιμο.
 Ισχύει τώρα,
Ισχύει τώρα, 
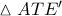 έχουμε
έχουμε 
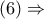


 και άρα, το τετράπλευρο
και άρα, το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο. έχουν κοινό περίκυκλο γιατί έχουν κοινά τα σημεία
έχουν κοινό περίκυκλο γιατί έχουν κοινά τα σημεία  , και περίκυκλός τους ταυτίζεται με τον περίκυκλο
, και περίκυκλός τους ταυτίζεται με τον περίκυκλο  του
του  , λόγω των κοινών πλέον σημείων
, λόγω των κοινών πλέον σημείων  .
.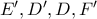 είναι ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
είναι ομοκυκλικά και το ζητούμενο έχει αποδειχθεί. του ως άνω κύκλου
του ως άνω κύκλου  , ταυτίζεται με τον "Βόρειο πόλο" του περίκυκλου
, ταυτίζεται με τον "Βόρειο πόλο" του περίκυκλου  του
του  , ως το σημείο τομής της διχοτόμου της εξωτερικής γωνίας
, ως το σημείο τομής της διχοτόμου της εξωτερικής γωνίας 
 λόγω του ισοσκελούς τραπεζίου
λόγω του ισοσκελούς τραπεζίου 
 και της μεσοκάθετης ευθείας της χορδής του
και της μεσοκάθετης ευθείας της χορδής του  , η οποία ταυτίζεται με την μεσοκάθετη ευθεία της διαμέτρου
, η οποία ταυτίζεται με την μεσοκάθετη ευθεία της διαμέτρου  του
του  .
.Ας δούμε και μια διαφορετική προσέγγιση του προβλήματοςΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Τετ Δεκ 01, 2021 2:55 pmΠερίκυκλος ισοτομικών.png
Έστωτα σημεία επαφής του έγκυκλου
ορθογωνίου στο
τριγώνου
με τις πλευρές του
αντίστοιχα. Να δειχθεί ότι ο περίκυκλος του τριγώνου
διέρχεται από το
, όπου
τα ισοτομικά των
αντίστοιχα ως προς τις πλευρές που ανήκουν
 Έστω
Έστω 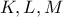 τα μέσα των πλευρών
τα μέσα των πλευρών  του
του  και
και  .
.  είναι η ακτίνα του εγγεγραμμένου κύκλου του ορθογωνίου τριγώνου
είναι η ακτίνα του εγγεγραμμένου κύκλου του ορθογωνίου τριγώνου  και η ημιπερίμετρός του αντίστοιχα , τότε ισχύει:
και η ημιπερίμετρός του αντίστοιχα , τότε ισχύει: 

 συνευθειακά οπότε με
συνευθειακά οπότε με 

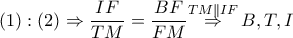 συνευθειακά, δηλαδή η
συνευθειακά, δηλαδή η  είναι η ευθεία της διχοτόμου της γωνίας
είναι η ευθεία της διχοτόμου της γωνίας 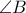 .
. (συμμετρία ως προς
(συμμετρία ως προς  )
)  (συμμετρίας ως προς την διχοτόμο
(συμμετρίας ως προς την διχοτόμο  ) και συνεπώς το τετράπλευρο
) και συνεπώς το τετράπλευρο  είναι εγγράψιμο σε κύκλο.
είναι εγγράψιμο σε κύκλο.  Αν
Αν  τότε έχουμε:
τότε έχουμε: 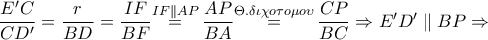
 ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
ομοκυκλικά και το ζητούμενο έχει αποδειχθεί. . Επομένως, σύμφωνα με γνωστό λήμμα (βλέπε το λήμμα 1 viewtopic.php?f=22&t=68789&p=334622#p334622) ο περιγεγραμμένος κύκλος του τριγώνου
. Επομένως, σύμφωνα με γνωστό λήμμα (βλέπε το λήμμα 1 viewtopic.php?f=22&t=68789&p=334622#p334622) ο περιγεγραμμένος κύκλος του τριγώνου 
 του τόξου
του τόξου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  ,
,  .
. .
Πράγματι, το τρίγωνο
.
Πράγματι, το τρίγωνο  είναι ορθογώνιο και ισοσκελές, οπότε
είναι ορθογώνιο και ισοσκελές, οπότε  .
. έχουμε:
έχουμε:
 .
. .
. το μέσο της
το μέσο της  . Τότε το τρίγωνο
. Τότε το τρίγωνο  ισοσκελές (εφόσον το
ισοσκελές (εφόσον το  υψος και διάμεσος),
υψος και διάμεσος), 
 είναι
είναι
 , από το οποίο προκύπτει το αποδεικτέο.
, από το οποίο προκύπτει το αποδεικτέο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες