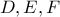 τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  κέντρου
κέντρου  με τις πλευρές
με τις πλευρές  αντίστοιχα τριγώνου
αντίστοιχα τριγώνου  . Να δειχθεί ότι
. Να δειχθεί ότι  , όπου
, όπου  το ορθόκεντρο του τριγώνου
το ορθόκεντρο του τριγώνου 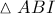 και
και  το μέσο της
το μέσο της 
Συντονιστές: vittasko, silouan, rek2
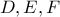 τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  κέντρου
κέντρου  με τις πλευρές
με τις πλευρές  αντίστοιχα τριγώνου
αντίστοιχα τριγώνου  . Να δειχθεί ότι
. Να δειχθεί ότι  , όπου
, όπου  το ορθόκεντρο του τριγώνου
το ορθόκεντρο του τριγώνου 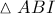 και
και  το μέσο της
το μέσο της 
ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Δευ Νοέμ 22, 2021 6:18 pmΈστωτα σημεία επαφής του έγκυκλου
κέντρου
με τις πλευρές
αντίστοιχα τριγώνου
. Να δειχθεί ότι
, όπου
το ορθόκεντρο του τριγώνου
και
το μέσο της

 Έστω
Έστω  , οι προβολές των σημείων
, οι προβολές των σημείων  , επί των ευθειών
, επί των ευθειών  αντιστοίχως και είναι γνωστό ότι τα σημεία αυτά ανήκουν στην ευθεία
αντιστοίχως και είναι γνωστό ότι τα σημεία αυτά ανήκουν στην ευθεία  .
. και ας είναι
και ας είναι  , το σημείο τομής των
, το σημείο τομής των  , αντί του
, αντί του 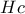 της εκφώνησης.
της εκφώνησης.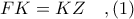 και ας είναι
και ας είναι  , το μέσον του
, το μέσον του  και άρα έχουμε
και άρα έχουμε 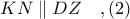
 Τα τρίγωνα
Τα τρίγωνα  τώρα, έχουν τις πλευρές τους κάθετες μία προς μία και άρα, οι ευθείες
τώρα, έχουν τις πλευρές τους κάθετες μία προς μία και άρα, οι ευθείες  , ως οι ομόλογες διάμεσοι αυτών των τριγώνων είναι κάθετες μεταξύ των.
, ως οι ομόλογες διάμεσοι αυτών των τριγώνων είναι κάθετες μεταξύ των.
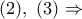
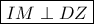 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. και έστω
και έστω 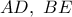 τα ύψη του και
τα ύψη του και  το ορθόκεντρό του. Η δια του σημείου
το ορθόκεντρό του. Η δια του σημείου  κάθετη ευθεία επί την
κάθετη ευθεία επί την  , επανατέμνει τον περίκυκλο έστω
, επανατέμνει τον περίκυκλο έστω  του τριγώνου
του τριγώνου  , στο σημείο
, στο σημείο  . Αποδείξτε ότι
. Αποδείξτε ότι  , όπου
, όπου  .
. Από
Από  και
και  , συμφωνα με το Θεώρημα Θαλή, προκύπτει άμεσα ότι ισχύει
, συμφωνα με το Θεώρημα Θαλή, προκύπτει άμεσα ότι ισχύει  και το Λήμμα έχει αποδειχθεί.
και το Λήμμα έχει αποδειχθεί.Ας δούμε και μια άλλη προσέγγιση στηριγμένη σε ένα «χορό κύκλων».ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Δευ Νοέμ 22, 2021 6:18 pmIM κάθετη στην DHc.png
Έστωτα σημεία επαφής του έγκυκλου
κέντρου
με τις πλευρές
αντίστοιχα τριγώνου
. Να δειχθεί ότι
, όπου
το ορθόκεντρο του τριγώνου
και
το μέσο της

 τα σημεία τομής των
τα σημεία τομής των  με τις
με τις  αντίστοιχα.
αντίστοιχα.  είναι ισοσκελή (τα ύψη τους είναι και αντίστοιχοι διχοτόμοι άρα και μεσοκάθετες ) οπότε και τα
είναι ισοσκελή (τα ύψη τους είναι και αντίστοιχοι διχοτόμοι άρα και μεσοκάθετες ) οπότε και τα 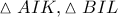 είναι ισοσκελή και με
είναι ισοσκελή και με  (κάθετες πλευρές του ίδιου προσανατολισμού) θα είναι και όμοια.
Με
(κάθετες πλευρές του ίδιου προσανατολισμού) θα είναι και όμοια.
Με  προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο σε κύκλο, οπότε
είναι εγγράψιμο σε κύκλο, οπότε  εγγράψιμο σε κύκλο, οπότε
εγγράψιμο σε κύκλο, οπότε  με
με  .
.  τα μέσα των
τα μέσα των  αντίστοιχα προκύπτει ότι
αντίστοιχα προκύπτει ότι  εγγράψιμο σε κύκλο και συνεπώς
εγγράψιμο σε κύκλο και συνεπώς 
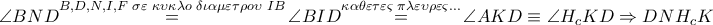 εγγράψιμο σε κύκλο , οπότε
εγγράψιμο σε κύκλο , οπότε  και συνεπώς το τετράπλευρο
και συνεπώς το τετράπλευρο  είναι εγγράψιμο σε κύκλο οπότε
είναι εγγράψιμο σε κύκλο οπότε  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.Ας δούμε και μια διαφορετική ("μετρική") αντιμετώπιση του προβλήματοςΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Δευ Νοέμ 22, 2021 6:18 pmIM κάθετη στην DHc.png
Έστωτα σημεία επαφής του έγκυκλου
κέντρου
με τις πλευρές
αντίστοιχα τριγώνου
. Να δειχθεί ότι
, όπου
το ορθόκεντρο του τριγώνου
και
το μέσο της

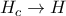 και ας είναι
και ας είναι  και ας είναι
και ας είναι  η ορθή προβολή του
η ορθή προβολή του  στην
στην  .
. για το τρίγωνο
για το τρίγωνο  (προς αποφυγήν των απολύτων τιμών) .
(προς αποφυγήν των απολύτων τιμών) . είναι ισοσκελή και συνεπώς
είναι ισοσκελή και συνεπώς  οπότε
οπότε 
 και από
και από  η
η  γίνεται
γίνεται ![A{{T}^{2}}=2{{c}^{2}}-2{{c}^{2}}\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}=\ldots \dfrac{c}{a}\left[ {{b}^{2}}-{{\left( a-c \right)}^{2}} \right]:\left( 2 \right) A{{T}^{2}}=2{{c}^{2}}-2{{c}^{2}}\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}=\ldots \dfrac{c}{a}\left[ {{b}^{2}}-{{\left( a-c \right)}^{2}} \right]:\left( 2 \right)](/forum/ext/geomar/texintegr/latexrender/pictures/8cae99da4b8af09a6ddf6b781e0e9979.png) Από
Από 
 με διατέμνουσα την
με διατέμνουσα την  θα έχουμε:
θα έχουμε: 





 σύμφωνα με το Stathis Koutras Theorem θα είναι
σύμφωνα με το Stathis Koutras Theorem θα είναι  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: KDORTSI και 10 επισκέπτες