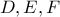 τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου
τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου  με τις πλευρές του
με τις πλευρές του  αντίστοιχα και ας είναι
αντίστοιχα και ας είναι  , με
, με  τον εγγεγραμμένο κύκλο . Να δειχθεί ότι το δεύτερο (εκτός του
τον εγγεγραμμένο κύκλο . Να δειχθεί ότι το δεύτερο (εκτός του  ) σημείο τομής
) σημείο τομής  των περίκυκλων των τριγώνων
των περίκυκλων των τριγώνων  ανήκει στην
ανήκει στην  , με
, με  το μέσο της
το μέσο της 
Συντονιστές: vittasko, silouan, rek2
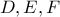 τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου
τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου  με τις πλευρές του
με τις πλευρές του  αντίστοιχα και ας είναι
αντίστοιχα και ας είναι  , με
, με  τον εγγεγραμμένο κύκλο . Να δειχθεί ότι το δεύτερο (εκτός του
τον εγγεγραμμένο κύκλο . Να δειχθεί ότι το δεύτερο (εκτός του  ) σημείο τομής
) σημείο τομής  των περίκυκλων των τριγώνων
των περίκυκλων των τριγώνων  ανήκει στην
ανήκει στην  , με
, με  το μέσο της
το μέσο της 
 και
και  και
και  σημείο του επιπέδου, τότε η συνάρτηση
σημείο του επιπέδου, τότε η συνάρτηση  είναι γραμμική, όπου
είναι γραμμική, όπου  η δύναμη σημείου, με
η δύναμη σημείου, με  το κέντρο του κύκλου
το κέντρο του κύκλου  και
και  την ακτίνα του. Η απόδειξη είναι απλώς πράξεις (φεύγουν οι όροι υψωμένοι στο τετράγωνο από τις εξισώσεις των κύκλων και μένουν μόνο γραμμικοί όροι).
την ακτίνα του. Η απόδειξη είναι απλώς πράξεις (φεύγουν οι όροι υψωμένοι στο τετράγωνο από τις εξισώσεις των κύκλων και μένουν μόνο γραμμικοί όροι).  , έστω
, έστω  , όπου
, όπου  (προσανατολισμένος λόγος), ισχύει
(προσανατολισμένος λόγος), ισχύει  .
. ο
ο  και
και  ο
ο  και
και  . Τότε θέλουμε να αποδείξουμε ότι
. Τότε θέλουμε να αποδείξουμε ότι  , οπότε το
, οπότε το  θα ανήκει στον ριζικό άξονα των κύκλων που είναι και το ζητούμενο.
θα ανήκει στον ριζικό άξονα των κύκλων που είναι και το ζητούμενο.  ανήκει στον ριζικό άξονα του
ανήκει στον ριζικό άξονα του  και του εγγεγραμμένου κύκλου και ο
και του εγγεγραμμένου κύκλου και ο  τέμνει το
τέμνει το  στο μέσο του
στο μέσο του  (πράγματι
(πράγματι  , δηλαδή το
, δηλαδή το  είναι ισοσκελές τραπέζιο, οπότε
είναι ισοσκελές τραπέζιο, οπότε  ).
). η ημιπερίμετρος:
η ημιπερίμετρος: 



 και
και  . Τότε
. Τότε 
 .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες