 , το οποίο κινείται σε ημικύκλιο διαμέτρου
, το οποίο κινείται σε ημικύκλιο διαμέτρου  , φέρουμε την εφαπτομένη και
, φέρουμε την εφαπτομένη και το κάθετο προς την εφαπτομένη τμήμα
 . Υπολογίστε το μέγιστο εμβαδόν του τριγώνου
. Υπολογίστε το μέγιστο εμβαδόν του τριγώνου  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , το οποίο κινείται σε ημικύκλιο διαμέτρου
, το οποίο κινείται σε ημικύκλιο διαμέτρου  , φέρουμε την εφαπτομένη και
, φέρουμε την εφαπτομένη και  . Υπολογίστε το μέγιστο εμβαδόν του τριγώνου
. Υπολογίστε το μέγιστο εμβαδόν του τριγώνου  .
. , έχουμε
, έχουμε  με
με 
 έχει εξίσωση
έχει εξίσωση  και η κάθετη από το
και η κάθετη από το 
 με
με 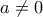 .
. , άρα
, άρα  και
και 


 έχει σταθερό άθροισμα, το γινόμενό τους γίνεται μέγιστο όταν είναι ανάλογοι των εκθετών τους:
έχει σταθερό άθροισμα, το γινόμενό τους γίνεται μέγιστο όταν είναι ανάλογοι των εκθετών τους: , άρα
, άρα 

 , έχουμε οριζόντια εφαπτομένη και
, έχουμε οριζόντια εφαπτομένη και  (μικρότερο από το ευρεθέν).
(μικρότερο από το ευρεθέν).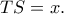 Από το εγγεγραμμένο
Από το εγγεγραμμένο  οι κόκκινες γωνίες είναι ίσες, οπότε τα ορθογώνια τρίγωνα
οι κόκκινες γωνίες είναι ίσες, οπότε τα ορθογώνια τρίγωνα  είναι όμοια. Αλλά, λόγω της εφαπτομένης είναι
είναι όμοια. Αλλά, λόγω της εφαπτομένης είναι  Άρα,
Άρα,  και
και  απ' όπου παίρνω την δεκτή ρίζα
απ' όπου παίρνω την δεκτή ρίζα 


 για
για 
 οι κόκκινες γωνίες είναι
οι κόκκινες γωνίες είναι  οι πράσινες
οι πράσινες  και
και 
 η προβολή του
η προβολή του  στην διάμετρο
στην διάμετρο  και
και  το κέντρο του ημικυκλίου . Θέτω
το κέντρο του ημικυκλίου . Θέτω  .
. 
 .
.  και είναι :
και είναι :  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 17 επισκέπτες