 εφάπτεται εσωτερικά και στους τρεις.
εφάπτεται εσωτερικά και στους τρεις. Από τυχόν σημείο
 του
του  φέρνουμε τα εφαπτόμενα τμήματα στους ίσους κύκλους. Να δείξετε ότι ένα από
φέρνουμε τα εφαπτόμενα τμήματα στους ίσους κύκλους. Να δείξετε ότι ένα από αυτά είναι ίσο με το άθροισμα των άλλων δύο.
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 εφάπτεται εσωτερικά και στους τρεις.
εφάπτεται εσωτερικά και στους τρεις.  του
του  φέρνουμε τα εφαπτόμενα τμήματα στους ίσους κύκλους. Να δείξετε ότι ένα από
φέρνουμε τα εφαπτόμενα τμήματα στους ίσους κύκλους. Να δείξετε ότι ένα από Ας δούμε και τη διαπραγμάτευση που ακολουθεί.george visvikis έγραψε: ↑Τρί Ιούλ 06, 2021 4:24 pmΤρεις ίσοι κύκλοι εφάπτονται εξωτερικά ανά δύο και ένας κύκλοςεφάπτεται εσωτερικά και στους τρεις.
Από τυχόν σημείοτου
φέρνουμε τα εφαπτόμενα τμήματα στους ίσους κύκλους. Να δείξετε ότι ένα από
αυτά είναι ίσο με το άθροισμα των άλλων δύο.
 , σημείο
, σημείο  εκτός αυτού, το εφαπτόμενο ευθύγραμμο τμήμα
εκτός αυτού, το εφαπτόμενο ευθύγραμμο τμήμα στον κύκλο και μία ευθεία διερχόμενη από το σημείο
στον κύκλο και μία ευθεία διερχόμενη από το σημείο  που τέμνει τον κύκλο στα σημεία
που τέμνει τον κύκλο στα σημεία  τότε, ισχύει
τότε, ισχύει

 παραλληλόγραμμο.
παραλληλόγραμμο. 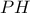 δηλαδή
δηλαδή  παραλληλόγραμμο.
παραλληλόγραμμο. 
 και για το σημείο
και για το σημείο  του "μικρού" τόξου
του "μικρού" τόξου  ,
, 

 προκύπτει και από την ομοιότητα των τετραπλαέυρων
προκύπτει και από την ομοιότητα των τετραπλαέυρων 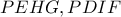 που μας οδηγεί στην εφαρμογή
που μας οδηγεί στην εφαρμογή 
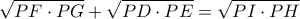
 ή με βάση τις
ή με βάση τις 
 ,
, 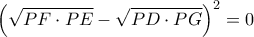
 που ισχύει λόγω της
που ισχύει λόγω της  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 7 επισκέπτες