 είναι ορθογώνιο και ισοσκελές , με υποτείνουσα
είναι ορθογώνιο και ισοσκελές , με υποτείνουσα  , η οποία έχει μέσο το σημείο
, η οποία έχει μέσο το σημείο  .
.Τα σημεία
 , είναι η προβολές των κορυφών
, είναι η προβολές των κορυφών  , πάνω σε μεταβλητή ευθεία διερχόμενη από το
, πάνω σε μεταβλητή ευθεία διερχόμενη από το  .
.α) Δείξτε ότι το άθροισμα :
 , μένει σταθερό . ... β) Υπολογίστε το μέγιστο του τμήματος
, μένει σταθερό . ... β) Υπολογίστε το μέγιστο του τμήματος  .
.
 . Το
. Το 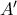 κινείται σε κύκλο διαμέτρου
κινείται σε κύκλο διαμέτρου  , ο οποίος εφάπτεται στη
, ο οποίος εφάπτεται στη  , αφού η διάμεσος
, αφού η διάμεσος  είναι ίσα, αφού
είναι ίσα, αφού  και
και  (υπό χoρδής κι εφαπτομένης και κατακορυφήν διαδοχικά),
(υπό χoρδής κι εφαπτομένης και κατακορυφήν διαδοχικά),  , οπότε
, οπότε 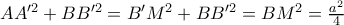 , σταθερό.
, σταθερό. ,
,  και
και 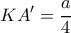 .
. 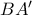 ισούται με
ισούται με  , δηλαδή μισό
, δηλαδή μισό  .
. ( σταθερό) ,
( σταθερό) ,  .
. ,
, 

 είναι σταθερό και το
είναι σταθερό και το  διαγράφει τον κύκλο διαμέτρου
διαγράφει τον κύκλο διαμέτρου  του
του  το αντιδιαμετρικό του
το αντιδιαμετρικό του  .
.