 έχουν εγγραφεί σε ισόπλευρο τρίγωνο πλευράς
έχουν εγγραφεί σε ισόπλευρο τρίγωνο πλευράς  , όπως φαίνεται στο σχήμα.
, όπως φαίνεται στο σχήμα.Να προσδιορίσετε το
 ως έκφραση του
ως έκφραση του  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 έχουν εγγραφεί σε ισόπλευρο τρίγωνο πλευράς
έχουν εγγραφεί σε ισόπλευρο τρίγωνο πλευράς  , όπως φαίνεται στο σχήμα.
, όπως φαίνεται στο σχήμα. ως έκφραση του
ως έκφραση του  .
. και
και  . Ο έγκυκλος
. Ο έγκυκλος  του ισοπλεύρου
του ισοπλεύρου 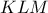 έχει
έχει 
 και αν
και αν  είναι ο έγκυκλος του
είναι ο έγκυκλος του  τότε
τότε 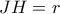
 σημείο επαφής με την
σημείο επαφής με την  Νόμος συνημιτόνου στο
Νόμος συνημιτόνου στο 





 Αντικαθιστώντας τώρα στην
Αντικαθιστώντας τώρα στην  παίρνω
παίρνω 
 οπότε
οπότε 
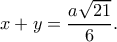 Εφαρμόζοντας τώρα το νόμο συνημιτόνου στο
Εφαρμόζοντας τώρα το νόμο συνημιτόνου στο 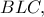 βρίσκω
βρίσκω  Κατασκευή:
Κατασκευή: του κύκλου
του κύκλου  και φέρνω από το μέσο
και φέρνω από το μέσο  της
της  κάθετη στη
κάθετη στη  που τέμνει το εν λόγω
που τέμνει το εν λόγω 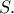 Ομοίως ορίζονται τα σημεία
Ομοίως ορίζονται τα σημεία  Οι
Οι 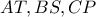 τέμνονται ανά δύο στα
τέμνονται ανά δύο στα 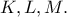 Οι 4 κύκλοι είναι οι
Οι 4 κύκλοι είναι οι  και ολοκληρώνεται η κατασκευή.
και ολοκληρώνεται η κατασκευή. Πράγματι, αν
Πράγματι, αν  είναι το σημείο τομής των
είναι το σημείο τομής των 
 και
και 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες