 και
και  το μέσο της
το μέσο της  Γράφω μεταβλητό κύκλο που διέρχεται από
Γράφω μεταβλητό κύκλο που διέρχεται από τα σημεία
 και τέμνει τις
και τέμνει τις  στα
στα 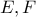 αντίστοιχα. Να βρείτε το μήκος
αντίστοιχα. Να βρείτε το μήκος  της προβολής του
της προβολής του  στην
στην  χρησιμοποιώντας όσο το δυνατόν λιγότερα από τα πρωτεύοντα στοιχεία του τριγώνου
χρησιμοποιώντας όσο το δυνατόν λιγότερα από τα πρωτεύοντα στοιχεία του τριγώνου 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 και
και  το μέσο της
το μέσο της  Γράφω μεταβλητό κύκλο που διέρχεται από
Γράφω μεταβλητό κύκλο που διέρχεται από  και τέμνει τις
και τέμνει τις  στα
στα 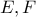 αντίστοιχα. Να βρείτε το μήκος
αντίστοιχα. Να βρείτε το μήκος  της προβολής του
της προβολής του  στην
στην  χρησιμοποιώντας όσο το δυνατόν λιγότερα από τα πρωτεύοντα στοιχεία του τριγώνου
χρησιμοποιώντας όσο το δυνατόν λιγότερα από τα πρωτεύοντα στοιχεία του τριγώνου 
george visvikis έγραψε: ↑Δευ Απρ 12, 2021 11:36 amΜε αφορμή αυτήν Μήκος προβολής.png
Δίνεται ισοσκελές τρίγωνοκαι
το μέσο της
Γράφω μεταβλητό κύκλο που διέρχεται από
τα σημείακαι τέμνει τις
στα
αντίστοιχα. Να βρείτε το μήκος
της προβολής του
στην
χρησιμοποιώντας όσο το δυνατόν λιγότερα από τα πρωτεύοντα στοιχεία του τριγώνου
 το, άλλο, σημείο τομής της
το, άλλο, σημείο τομής της  με τον κύκλο.
με τον κύκλο. και επειδή
και επειδή  προσθέτω κατά μέλη , κι έχω:
προσθέτω κατά μέλη , κι έχω: 
 κι εδώ προσθέτω κι έχω:
κι εδώ προσθέτω κι έχω:  και η
και η  δίδει:
δίδει:  . Η σχέση, νομίζω , γράφεται :
. Η σχέση, νομίζω , γράφεται : 
 το άλλο σημείο τομής της
το άλλο σημείο τομής της  με τον κύκλο, τότε είναι
με τον κύκλο, τότε είναι
 ,
, 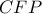 είναι όμοια και κατ' ακολουθία όλες οι προφανείς ομοιότητες εκ του σχήματος. οπότε είναι
είναι όμοια και κατ' ακολουθία όλες οι προφανείς ομοιότητες εκ του σχήματος. οπότε είναι
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες