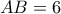 και
και  ενός κύκλου , είναι κάθετες . Σημείο
ενός κύκλου , είναι κάθετες . Σημείο  κινείται στο ημικύκλιο που δεν
κινείται στο ημικύκλιο που δενπεριέχει το
 . Αν
. Αν  είναι το μέσο της χορδής
είναι το μέσο της χορδής  , υπολογίστε το μέγιστο μήκος του τμήματος
, υπολογίστε το μέγιστο μήκος του τμήματος  .
.Σημείωση : Την ώρα που γράφω την άσκηση γίνεται μεγάλος σεισμός
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
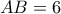 και
και  ενός κύκλου , είναι κάθετες . Σημείο
ενός κύκλου , είναι κάθετες . Σημείο  κινείται στο ημικύκλιο που δεν
κινείται στο ημικύκλιο που δεν . Αν
. Αν  είναι το μέσο της χορδής
είναι το μέσο της χορδής  , υπολογίστε το μέγιστο μήκος του τμήματος
, υπολογίστε το μέγιστο μήκος του τμήματος  .
.Θ Πτολεμαίου στο τετράπλευρο
 , Π. Θ. στο
, Π. Θ. στο  και πρώτο θ. διαμέσων
και πρώτο θ. διαμέσων  με
με  έχω:
έχω: 
 την μέγιστη διάμεσο :
την μέγιστη διάμεσο :
 διαγράφει σταθερό κύκλο και η μεγιστοποίηση πιάνεται όταν ευθεία της διαμέσου διέρχεται από το κέντρο του
Η ακτίνα του κύκλου με κέντρο το
διαγράφει σταθερό κύκλο και η μεγιστοποίηση πιάνεται όταν ευθεία της διαμέσου διέρχεται από το κέντρο του
Η ακτίνα του κύκλου με κέντρο το  είναι :
είναι : 
Θέτω
 Είναι
Είναι 

 όπου με παραγώγους βρίσκω
όπου με παραγώγους βρίσκω  για
για 
 κι έχασα αρκετό χρόνο προσπαθώντας να το αποδείξω. Η προσέγγιση
κι έχασα αρκετό χρόνο προσπαθώντας να το αποδείξω. Η προσέγγιση 
 . Αυτός είναι
. Αυτός είναι  , που βλέπετε στο σχήμα ( εδώ μεταφέρεται τώρα το πρόβλημα ) .
, που βλέπετε στο σχήμα ( εδώ μεταφέρεται τώρα το πρόβλημα ) .
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες